Engineers should definitely take a peek, and not only them!
1. Area Moment of Inertia
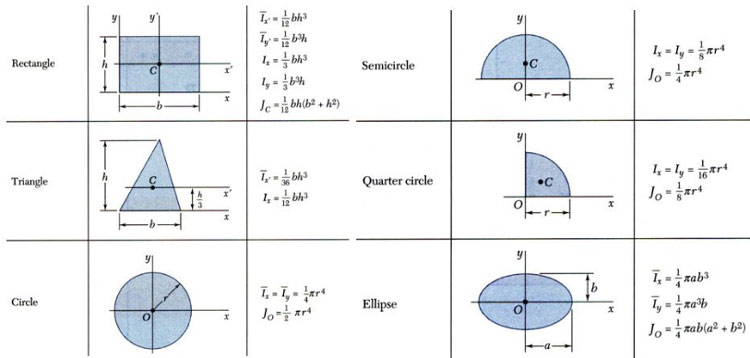 The second moment of area, also known as moment of inertia of plane area, area moment of inertia, polar moment of area or second area moment, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis.
The second moment of area, also known as moment of inertia of plane area, area moment of inertia, polar moment of area or second area moment, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis.
The second moment of area for a shape is easier to be calculated with respect to a parallel axis or with respect to a perpendicular axis through the centroid of the shape.
Many formulas exist for Area Moment of Inertia. You can find all of the Area Moment of Inertia equations that exist in fxSolver's database in this LINK.
2. Angular Acceleration
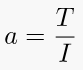
Moment of inertia is the mass property of a rigid body that determines the torque needed for a desired angular acceleration about an axis of rotation.
Angular acceleration is the rate of change of angular velocity over time.
For all constant values of the torque of an object, the angular acceleration will also be constant. The constant angular acceleration can be calculated by the ratio of the total the torque of the object to the its moment of inertia.
3. Cantilever Euler Beam – Displacement
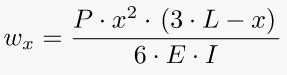
4. Catenary curve
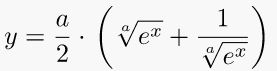
5. Center of mass (for a system of n-particles)
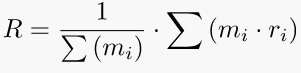
The barycentric coordinate system is a coordinate system in which the location of a point of a simplex (a triangle, tetrahedron, etc.) is specified as the center of mass, or barycenter, of masses placed at its vertices. Coordinates also extend outside the simplex, where one or more coordinates become negative.
The coordinates R of the center of mass of a n-particle system can be computed by the masses of the particles and their distances from a fixed point.
6. Compound pendulum ( ordinary frequency )
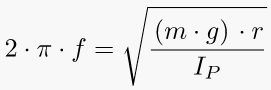
If you are interested in Pendulums you should definitely check the following posts: Pendulum and its Period and Pendulum Clocks.
7. Critical Damping Coefficient
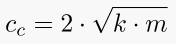
8. Elastic Potential Energy
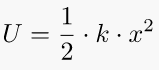
9. Half Sphere Mass
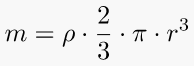
10. Kinetic Friction
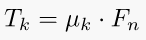
10+1. Rotational stiffness
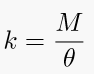
The stiffness of a body is a measure of the resistance offered by an elastic body to deformation. For an elastic body with a single degree of freedom (for example, stretching or compression of a rod), the stiffness is depended on the force applied on the body and the displacement produced by the force.
You can try to search whatever you want just by clicking on the “Browse Formulas” button on the top left of your screen.
If you need any help, you will find some in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.
