Trigonometry is one of the core courses school students study in numerous countries accross the globe. We searched and found the 10 most useful formulas a school student might encounter. 

1. Pythagorean theorem (right triangle)

Determines the length of the hypotenuse of a right triangle based on the lengths of the other two sides. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. The Pythagorean equation relates the sides of a right triangle in a simple way, so that if the lengths of any two sides are known the length of the third side can be found. 

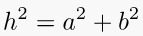
2. Area of an arbitrary triangle

The area of an arbitrary triangle can be calculated from the two sides of the triangle and the included angle. (Check the image in this LINK)

3. Area of a triangle (related to the two of its altitudes)

Altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base (the opposite side of the triangle). The area of the triangle can be calculated by the two of its altitudes and the sine an angle. S is the area of the triangle, h the altitudes and C the angle of the opposite side

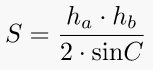
4. Hyperbolic triangle ( length of the base)

A hyperbolic sector is a region of the Cartesian plane {(x,y)} bounded by rays from the origin to two points (a, 1/a) and (b, 1/b) and by the hyperbola xy =1.
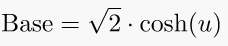
When in standard position, a hyperbolic sector determines a hyperbolic triangle, the right triangle with one vertex at the origin, base on the diagonal ray y = x, and third vertex on the hyperbola then xy =1. The length of the base of the hyperbolic triangle is propotional to the cosh(u).

5. Hyperbolic triangle ( length of the altitude)

As above, but the altitude of the hyperbolic triangle is proportional to the sinh(u).

6. Cosine function

The trigonometric functions are functions of an angle. They relate the angles of a triangle to the lengths of its sides. The most familiar trigonometric functions are the sine, cosine, and tangent. To define the trigonometric functions for an angle , start with any right triangle that contains this angle . The three sides of the triangle are named:
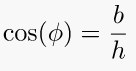
1) hypotenuse (is the side opposite the right angle and always the longest side of the right-angled triangle).
2) opposite side (is the side opposite to the angle we are interested in)
3) adjacent side (Is the side having both the angles of interest ).
The cosine is defined as the ratio of the side adjacent an angle of a right angled triangle to it’s hypotenuse.
Check the image in this LINK to understand it completely.

7. Double angle's sine (related to the sine and cosine)

Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, these are identities involving certain functions of one or more angles.
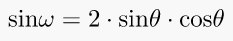
The sine of an angle is defined in the context of a right triangle, as the ratio of the length of the side that is opposite to the angle divided by the length of the longest side of the triangle (the hypotenuse ).
The cosine of an angle is also defined in the context of a right triangle, as the ratio of the length of the side the angle is in divided by the length of the longest side of the triangle (the hypotenuse ).
The tangent (tan) of an angle is the ratio of the sine to the cosine.

8. Ordinate of a point of a circle (trigonometric function)

The ordinate of point of a circle, in an x–y Cartesian coordinate system, can be computed by the ordinate of the center of the circle, the radius and the angle that the ray from the center of the circle to the point makes with the x-axis

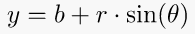
9. Rhombus area (trigonometric function)

A rhombus , is a simple (non-self-intersecting) quadrilateral all of whose four sides have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. 
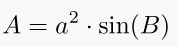
The area of a rhombus,can be calculated by the side and the sinus of any angle of the rhombus.

10. Flattening – 1st variant

Flattening is a measure of the compression of a circle or sphere along a diameter to form an ellipse or an ellipsoid of revolution (spheroid) respectively. Other terms used are ellipticity, or oblateness. The compression factor is b/a in each case. For the ellipse, this factor is also the aspect ratio of the ellipse.

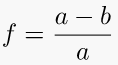
You can try to search whatever you want just by clicking on the “Browse Formulas” button on the top left of your screen.

If you need any help, you will find some in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.