Ballistics is the science of mechanics that deals with the launching, flight, behavior, and effects of projectiles, especially bullets, gravity bombs, rockets even baseballs. Here are the 10 equations you should have in mind if you are working on ballistics.
1. Escape Velocity
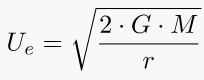
2. Trajectory Height
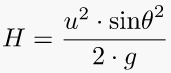
3. Trajectory Range
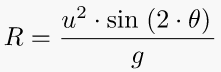
4. Range of a projectile
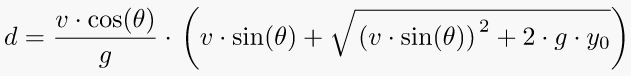
5. Angle of elevation
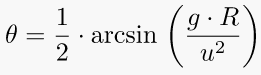
6. Angle required to hit for a projectile following a ballistic trajectory (coordinate (x,y))
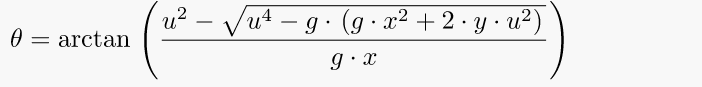
To hit a target at range x and altitude y when fired from (0,0) and with initial speed u the required angle of launch is depended on the initial velocity.
7. Ballistic Coefficient – using body length
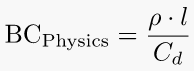
8. Ballistic Coefficient – using corss-sectional area
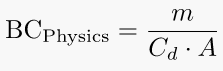
9. Velocity at a distance x (for object following a ballistic trajectory)
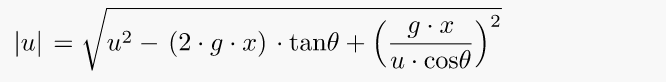
10. Time of flight for a projectile following a ballistic trajectory
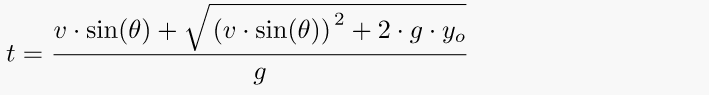
You can try to search whatever you want just by clicking on the “Browse Formulas” button on the top left of your screen.
If you need any help, you will find some in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.
