Flag! A piece of fabric that defines a place and a (usually) large group of people! From football club flags to National flags many events have occurred due to their existence, or they are just used as an excuse for some not so friendly and loving events!
But who says that a piece of cloth can't be fun?
Dr. Sheldon Cooper proves with his show that they are a hoot!
There are databases all over the internet with flag identification methods and other fun stuff.
But how is this relevant to an Equation Solver Webpage, such as fxSolver!
Well, the British flag theorem made it relevant, and also FUN!
Rectangle is any quadrilateral with four right angles. It can also be defined as an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°).
In Euclidean geometry, the British flag theorem says that if a point P is chosen inside rectangle ABCD, then the sum of the squared Euclidean distances from P to two opposite corners of the rectangle equals the sum to the other two opposite corners. (See equation on the left, where AP is the distance from P to the corner A in meters, CP the distance from P to the corner C, BP the distance from P to the corner B and DP the distance from P to the corner D in meters like all the other distances of the theorem).
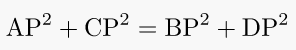
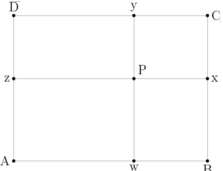The theorem also applies to points outside the rectangle, and more generally to the distances from a point in Euclidean space to the corners of a rectangle embedded into the space. Even more generally, if the sums of squared distances from a point P to the two pairs of opposite corners of a parallelogram are compared, the two sums will not in general be equal, but the difference of the two sums will depend only on the shape of the parallelogram and not on the choice of P.
The proof of that is pretty straight forward:
Drop perpendicular lines from the point P to the sides of the rectangle, meeting sides AB, BC, CD, and AD in points w, x, y and z respectively, as shown in the figure; these four points wxyz form the vertices of anorthodiagonal quadrilateral. By applying the Pythagorean theorem to the right triangle AwP, and observing that wP = Az, it follows that
AP2=Aw2+wP2=Aw2+Az2
By a similar argument the squared lengths of the distances from P to the rest of the corners are :
PC2=wB2+zD2
BP2=wB2+Az2
PD2=zD2+Aw2
Therefore:
AP2+PC2= (Aw2 + Az2)+(wB2+zD2)= (wB2 + Az2)+(zD2+Aw2)= BP2 + PD2
Go ahead, check this equation and search whatever else you want to solve. You will find some help in our fxSolver video.
Also remember to follow or interact with us in our social media pages. You will find links below.