Search results

The awe‐inspiring Great Pyramid of Cheops was built more than 4500 years ago. Its square base, originally 230 m on a side, covered 13.1 acres, and it was 146 m high (H), with a mass of about 7×10^9 kg. (The pyramid’s dimensions are slightly different today due to quarrying and some sagging). Historians estimate that 20,000 workers spent 20 years to construct it, working 12-hour days, 330 days per year.

a) Calculate the gravitational potential energy stored in the pyramid, given its center of mass is at one-fourth its height.

b) Only a fraction of the workers lifted blocks; most were involved in support services such as building ramps, bringing food and water, and hauling blocks to the site. Calculate the efficiency of the workers who did the lifting, assuming there were 1000 of them and they consumed food energy at the rate of 300 Kcal/hour.

first we calculate the number of hours worked per year.

then we calculate the number of hours worked in the 20 years.

Then we calculate the energy consumed in 20 years knowing the energy consumed per hour and the total hours worked in 20 years.

The efficiency is the resulting potential energy divided by the consumed energy.

A typical small rescue helicopter, like the one in the Figure below, has four blades, each is 4.00 m long and has a mass of 50.0 kg. The blades can be approximated as thin rods that rotate about one end of an axis perpendicular to their length. The helicopter has a total loaded mass of 1000 kg. (a) Calculate the rotational kinetic energy in the blades when they rotate at 300 rpm. (b) Calculate the translational kinetic energy of the helicopter when it flies at 20.0 m/s, and compare it with the rotational energy in the blades. (c) To what height could the helicopter be raised if all of the rotational kinetic energy could be used to lift it?

The first image shows how helicopters store large amounts of rotational kinetic energy in their blades. This energy must be put into the blades before takeoff and maintained until the end of the flight. The engines do not have enough power to simultaneously provide lift and put significant rotational energy into the blades.
The second image shows a helicopter from the Auckland Westpac Rescue Helicopter Service. Over 50,000 lives have been saved since its operations beginning in 1973. Here, a water rescue operation is shown. (credit: 111 Emergency, Flickr)

Strategy

Rotational and translational kinetic energies can be calculated from their definitions. The last part of the problem relates to the idea that energy can change form, in this case from rotational kinetic energy to gravitational potential energy.

Solution for (a)

We must convert the angular velocity to radians per second and calculate the moment of inertia before we can find E_r . The angular velocity ω for 1 r.p.m is

and for 300 r.p.m

The moment of inertia of one blade will be that of a thin rod rotated about its end.

The total I is four times this moment of inertia, because there are four blades. Thus,

and so The rotational kinetic energy is

Solution for (b)

Translational kinetic energy is defined as

To compare kinetic energies, we take the ratio of translational kinetic energy to rotational kinetic energy. This ratio is

Solution for (c)

At the maximum height, all rotational kinetic energy will have been converted to gravitational energy. To find this height, we equate those two energies:

Discussion

The ratio of translational energy to rotational kinetic energy is only 0.380. This ratio tells us that most of the kinetic energy of the helicopter is in its spinning blades—something you probably would not suspect. The 53.7 m height to which the helicopter could be raised with the rotational kinetic energy is also impressive, again emphasizing the amount of rotational kinetic energy in the blades.

Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/

Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in the figure below, and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.

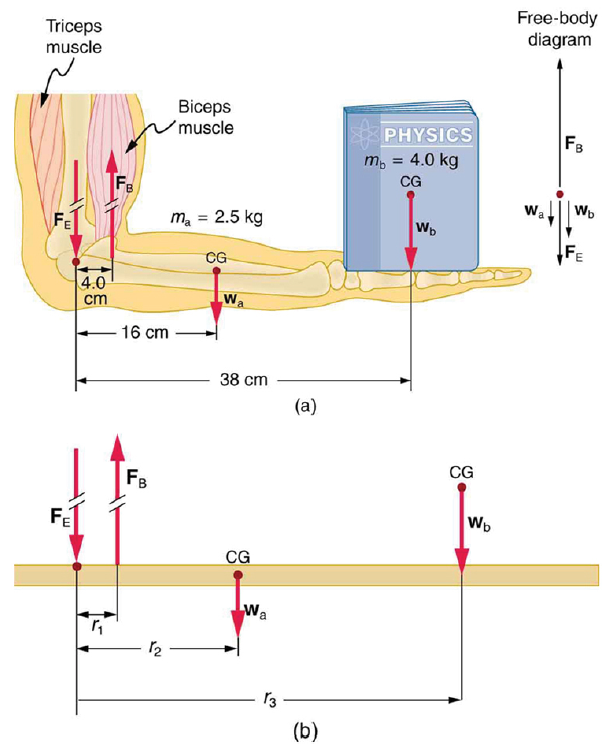
(a) The figure shows the forearm of a person holding a book. The biceps exert a force F_B to support the weight of the forearm and the book. The triceps are assumed to be relaxed. (b) Here, you can view an approximately equivalent mechanical system with the pivot at the elbow joint

Strategy

There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is F_B, that of the elbow joint is F_E, that of the weights of the forearm is w_a , and its load is w_b. Two of these are unknown F_B, so that the first condition for equilibrium cannot by itself yield F_B . But if we use the second condition and choose the pivot to be at the elbow, then the torque due to F_E is zero, and the only unknown becomes F_B .

Solution

The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium (net τ = 0) becomes

Note that sin θ = 1 for all forces, since θ = 90º for all forces. This equation can easily be solved for F_B in terms of known quantities,yielding. Entering the known values gives

which yields

Now, the combined weight of the arm and its load is known, so that the ratio of the force exerted by the biceps to the total weight is

Discussion

This means that the biceps muscle is exerting a force 7.38 times the weight supported.

Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/

Astrology, that unlikely and vague pseudoscience, makes much of the position of the planets at the moment of one’s birth. The only known force a planet exerts on Earth is gravitational.

(a) Calculate the gravitational force exerted on a 4.20 kg baby by a 100 kg father 0.200 m away at birth (he is assisting, so he is close to the child).

(b) Calculate the force on the baby due to Jupiter if it is at its closest distance to Earth, some 6.29e+11 m away. How does the force of Jupiter on the baby compare to the force of the father on the baby?

Father’s gravitational force on the baby is:

Jupiter’s gravitational force on the baby is:

(c) What should be the father’s weight, so that he exerts the same force on the baby as that of Jupiter? **
**this section is not included in the Reference material

Discussion

Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/

Dedicated to little Konstantinos