Moment of Inertia - Rod end
Description
Moment of inertia is the mass property of a rigid body that determines the torque needed for a desired angular acceleration about an axis of rotation. Moment of inertia depends on the shape of the body and may be different around different axes of rotation. A larger moment of inertia around a given axis requires more torque to increase the rotation, or to stop the rotation, of a body about that axis. The mass moment of inertia, usually denoted by I, measures the extent to which an object resists rotational acceleration about an axis, and is the rotational analogue to mass. For simple objects with geometric symmetry, one can often determine the moment of inertia in an exact closed-form expression. An infinitely thin (but rigid) rod or wire of length L and mass m, having axis of rotation at the end of the rod has moment of inertia depended on its mass and its length. (This formula applies also to special case of the thin rectangular plate with axis of rotation at the end of the plate, with h = L and w = 0. 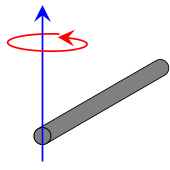
Variables
| Iend | Moment of Inertia of a rod (kg*m2) |
| m | Mass (kg) |
| L | Length of rod (m) |