Search results
A threaded rod, also known as a stud, is a relatively long rod that is threaded on both ends; the thread may extend along the complete length of the ... more
A threaded rod, also known as a stud, is a relatively long rod that is threaded on both ends; the thread may extend along the complete length of the ... more
Capital market line (CML) is the tangent line drawn from the point of the risk-free asset to the feasible region for risky ... more
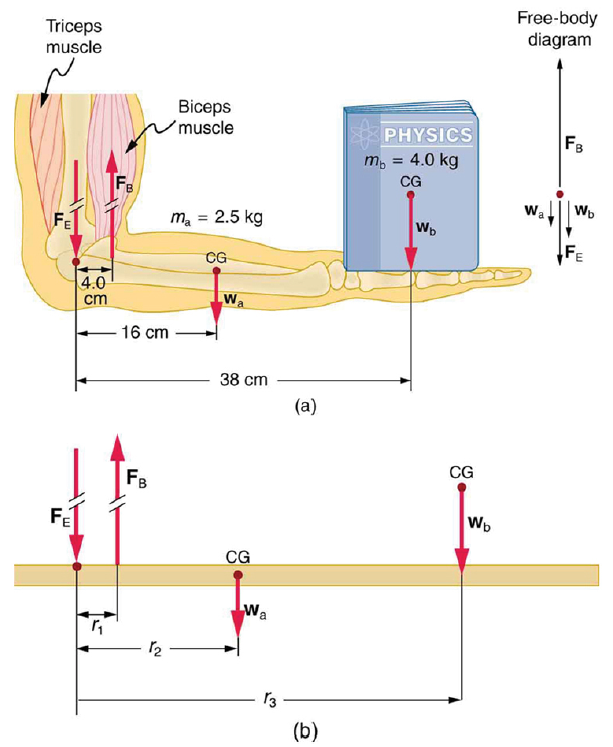
(a) The figure shows the forearm of a person holding a book. The biceps exert a force FB to support the weight of the forearm and the book. The triceps are assumed to be relaxed. (b) Here, you can view an approximately equivalent mechanical system with the pivot at the elbow joint
Strategy
There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is FB, that of the elbow joint is FE, that of the weights of the forearm is wa , and its load is wb. Two of these are unknown FB, so that the first condition for equilibrium cannot by itself yield FB . But if we use the second condition and choose the pivot to be at the elbow, then the torque due to FE is zero, and the only unknown becomes FB .
Solution
The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium (net τ = 0) becomes
Note that sin θ = 1 for all forces, since θ = 90º for all forces. This equation can easily be solved for FB in terms of known quantities,yielding. Entering the known values gives
which yields
Now, the combined weight of the arm and its load is known, so that the ratio of the force exerted by the biceps to the total weight is
Discussion
This means that the biceps muscle is exerting a force 7.38 times the weight supported.
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
David Sarnoff (Belarusian: Даві́д Сарно́ў, Russian: Дави́д Сарно́в, February 27, 1891 – December 12, 1971) was an American businessman and pioneer of ... more
The most common meaning of ripple in electrical science is the small unwanted residual periodic variation of the direct current (DC) output of a power ... more
The most common meaning of ripple in electrical science is the small unwanted residual periodic variation of the direct current (DC) output of a power ... more
A typical small rescue helicopter, like the one in the Figure below, has four blades, each is 4.00 m long and has a mass of 50.0 kg. The blades can be approximated as thin rods that rotate about one end of an axis perpendicular to their length. The helicopter has a total loaded mass of 1000 kg. (a) Calculate the rotational kinetic energy in the blades when they rotate at 300 rpm. (b) Calculate the translational kinetic energy of the helicopter when it flies at 20.0 m/s, and compare it with the rotational energy in the blades. (c) To what height could the helicopter be raised if all of the rotational kinetic energy could be used to lift it?

The first image shows how helicopters store large amounts of rotational kinetic energy in their blades. This energy must be put into the blades before takeoff and maintained until the end of the flight. The engines do not have enough power to simultaneously provide lift and put significant rotational energy into the blades.
The second image shows a helicopter from the Auckland Westpac Rescue Helicopter Service. Over 50,000 lives have been saved since its operations beginning in 1973. Here, a water rescue operation is shown. (credit: 111 Emergency, Flickr)
Strategy
Rotational and translational kinetic energies can be calculated from their definitions. The last part of the problem relates to the idea that energy can change form, in this case from rotational kinetic energy to gravitational potential energy.
Solution for (a)
We must convert the angular velocity to radians per second and calculate the moment of inertia before we can find Er . The angular velocity ω for 1 r.p.m is
and for 300 r.p.m
The moment of inertia of one blade will be that of a thin rod rotated about its end.
The total I is four times this moment of inertia, because there are four blades. Thus,
and so The rotational kinetic energy is
Solution for (b)
Translational kinetic energy is defined as
To compare kinetic energies, we take the ratio of translational kinetic energy to rotational kinetic energy. This ratio is
Solution for (c)
At the maximum height, all rotational kinetic energy will have been converted to gravitational energy. To find this height, we equate those two energies:
Discussion
The ratio of translational energy to rotational kinetic energy is only 0.380. This ratio tells us that most of the kinetic energy of the helicopter is in its spinning blades—something you probably would not suspect. The 53.7 m height to which the helicopter could be raised with the rotational kinetic energy is also impressive, again emphasizing the amount of rotational kinetic energy in the blades.
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
The Kelvin–Helmholtz mechanism is an astronomical process that occurs when the surface of a star or a planet cools. The cooling causes the pressure to ... more
Purchasing power (sometimes retroactively called adjusted for inflation) is the number of goods or services that can be purchased with a unit of currency. ... more
...can't find what you're looking for?
Create a new formula
Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in the figure below, and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.