Search results
When a driver is driving on a sag curve at night, the sight distance is limited by the higher grade in front of the vehicle. This distance must be long ... more
When a driver is driving on a sag curve at night, the sight distance is limited by the higher grade in front of the vehicle. This distance must be long ... more
In physics, the kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a ... more
Strategy for (a)
To find the buoyant force, we must find the weight of water displaced. We can do this by using the densities of water and steel given in Table [insert table #] We note that, since the steel is completely submerged, its volume and the water’s volume are the same. Once we know the volume of water, we can find its mass and weight
First, we use the definition of density to find the steel’s volume, and then we substitute values for mass and density. This gives :
Because the steel is completely submerged, this is also the volume of water displaced, Vw. We can now find the mass of water displaced from the relationship between its volume and density, both of which are known. This gives:
By Archimedes’ principle, the weight of water displaced is m w g , so the buoyant force is:
The steel’s weight is 9.80×10 7 N , which is much greater than the buoyant force, so the steel will remain submerged.
Strategy for (b)
Here we are given the maximum volume of water the steel boat can displace. The buoyant force is the weight of this volume of water.
The mass of water displaced is found from its relationship to density and volume, both of which are known. That is:
The maximum buoyant force is the weight of this much water, or
Discussion
The maximum buoyant force is ten times the weight of the steel, meaning the ship can carry a load nine times its own weight without sinking.
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
An elastic collision is an encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total ... more
An elastic collision is an encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total ... more
A collision is an isolated event in which two or more moving bodies (colliding bodies) exert forces on each other for a relatively short time. Collision is ... more
Porosity or void fraction is a measure of the void (i.e., “empty”) spaces in a material, and is a fraction of the volume of voids over the ... more
Prior to manned space flights, rocket sleds were used to test aircraft, missile equipment, and physiological effects on human subjects at high speeds. They consisted of a platform that was mounted on one or two rails and propelled by several rockets. Calculate the magnitude of force exerted by each rocket, called its thrust T , for the four-rocket propulsion system shown in the Figure below. The sled’s initial acceleration is 49 m/s 2, the mass of the system is 2100 kg, and the force of friction opposing the motion is known to be 650 N.
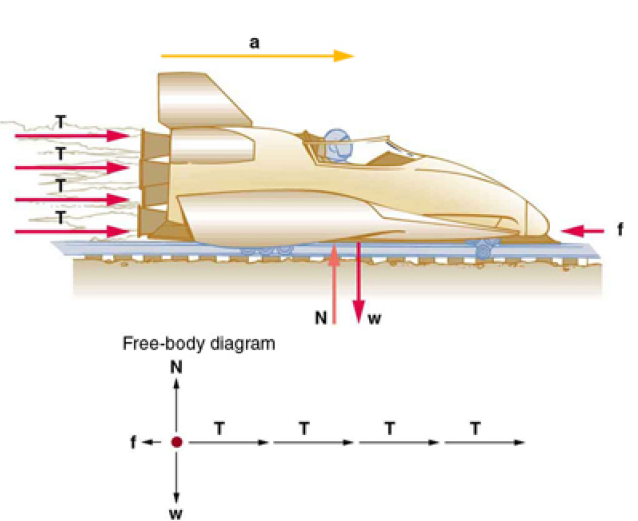
A sled experiences a rocket thrust that accelerates it to the right.Each rocket creates an identical thrust T . As in other situations where there is only horizontal acceleration, the vertical forces cancel. The ground exerts an upward force N on the system that is equal in magnitude and opposite in direction to its weight,w.The system here is the sled, its rockets, and rider, so none of the forces between these objects are considered. The arrow representing friction ( f ) is drawn larger than scale.
Assumptions: The mass of the Sled remains steady throughout the operation
Strategy
Although there are forces acting vertically and horizontally, we assume the vertical forces cancel since there is no vertical acceleration. This leaves us with only horizontal forces and a simpler one-dimensional problem. Directions are indicated with plus or minus signs, with right taken as the positive direction. See the free-body diagram in the figure.
Solution
Since acceleration, mass, and the force of friction are given, we start with Newton’s second law and look for ways to find the thrust of the engines. Since we have defined the direction of the force and acceleration as acting “to the right,” we need to consider only the magnitudes of these quantities in the calculations. Hence we begin with
Fnet is the net force along the horizontal direction, m is the rocket’s mass and a the acceleration.
We can see from the Figure at the top, that the engine thrusts add, while friction opposes the thrust.
Tt is the total thrust from the 4 rockets, Fnet the net force along the horizontal direction and Ff the force of friction.
Finally, since there are 4 rockets, we calculate the thrust that each one provides:
T is the individual Thrust of each engine, b is the number of rocket engines
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
The steering ratio is the relationship between how far you turn a steering wheel and how far the actual wheels turn as a result. A higher steering ratio ... more
...can't find what you're looking for?
Create a new formula
(a) Calculate the buoyant force on 10,000 metric tons (1.00×10 7 kg) of solid steel completely submerged in water, and compare this with the steel’s weight.
(b) What is the maximum buoyant force that water could exert on this same steel if it were shaped into a boat that could displace 1.00×10 5 m 3 of water?