Search results
To rotate the position of the character, we can imagine it as a point on a circle, and we will change the angle of the point by 20 degrees. To do so, we first need to find the radius of this circle and the original angle.
Drawing a right triangle inside the circle, we can find the radius using the Pythagorean Theorem:
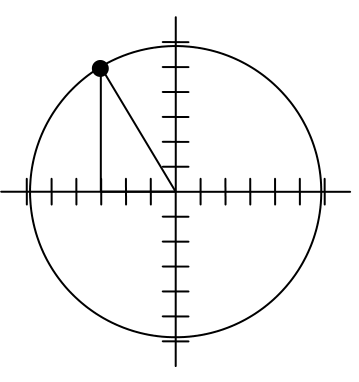
To find the angle, we need to decide first if we are going to find the acute angle of the triangle, the reference angle, or if we are going to find the angle measured in standard position. While either approach will work, in this case we will do the latter. By applying the cosine function and using our given information we get
While there are two angles that have this cosine value, the angle of 120.964 degrees is in the second quadrant as desired, so it is the angle we were looking for.
Rotating the point clockwise by 20 degrees, the angle of the point will decrease to 100.964 degrees. We can then evaluate the coordinates of the rotated point
For x axis:
For y axis:
The coordinates of the character on the rotated map will be (-1.109, 5.725)
Reference : PreCalculus: An Investigation of Functions,Edition 1.4 © 2014 David Lippman and Melonie Rasmussen
http://www.opentextbookstore.com/precalc/
Creative Commons License : http://creativecommons.org/licenses/by-sa/3.0/us/
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. If the internal ... more
The law of tangents is a statement about the relationship between the tangents of two angles of a triangle and the lengths of the opposing sides.The law of ... more
A triangle is a polygon with three edges and three vertices. In a scalene triangle, all sides are unequal and equivalently all angles are unequal. The area ... more
An angle bisector divides the angle into two angles with equal measures. An angle only has one bisector. Each point of an angle bisector is equidistant ... more
The law of cosines relates the cosine of an angle to the opposite side of an arbitrary triangle and the length of the triangle’s sides.
The law
... more
A right triangle (American English) or right-angled triangle (British English) is a triangle in which one angle is a right angle (that is, a 90-degree ... more
Altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base (the opposite side of the triangle). The area of ... more
Law of sines is an equation relating the lengths of the sides of any shaped triangle to the sines of its angles. The law of sines can be used to compute ... more
The area of an arbitrary triangle can be calculated from the two sides of the triangle and the included angle.... more
...can't find what you're looking for?
Create a new formula
In a video game design, a map shows the location of other characters relative to the player, who is situated at the origin, and the direction they are facing. A character currently shows on the map at coordinates (-3, 5). If the player rotates counterclockwise by 20 degrees, then the objects in the map will correspondingly rotate 20 degrees clockwise. Find the new coordinates of the character.