Euler line (distance between the centroid and the circumcenter of a triangle)
Description
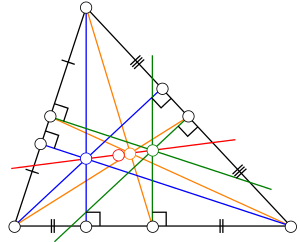
In geometry, the Euler line is a line determined from any triangle that is not equilateral. It passes through several important points determined from the triangle, including the orthocenter, the circumcenter, the centroid, the Exeter point and the center of the nine-point circle of the triangle. In any triangle, the orthocenter, circumcenter and centroid are collinear. The squared distance between the centroid and the circumcenter along the Euler line is less than the squared circumradius by an amount equal to one-ninth the sum of the squares of the side lengths a, b, and c.
Variables
| GO | The distance between the centroid and the circumcenter of the triangle (m) |
| R | The circumradius of the triangle (radius of the circle which passes through all the vertices of the triangle) (m) |
| a | Side of the triangle opposite to angle A (m) |
| b | Side of the triangle opposite to angle B (m) |
| c | Side of the triangle opposite to angle C (m) |