Search results

Prior to manned space flights, rocket sleds were used to test aircraft, missile equipment, and physiological effects on human subjects at high speeds. They consisted of a platform that was mounted on one or two rails and propelled by several rockets. Calculate the magnitude of force exerted by each rocket, called its thrust T , for the four-rocket propulsion system shown in the Figure below. The sled’s initial acceleration is 49 m/s ², the mass of the system is 2100 kg, and the force of friction opposing the motion is known to be 650 N.

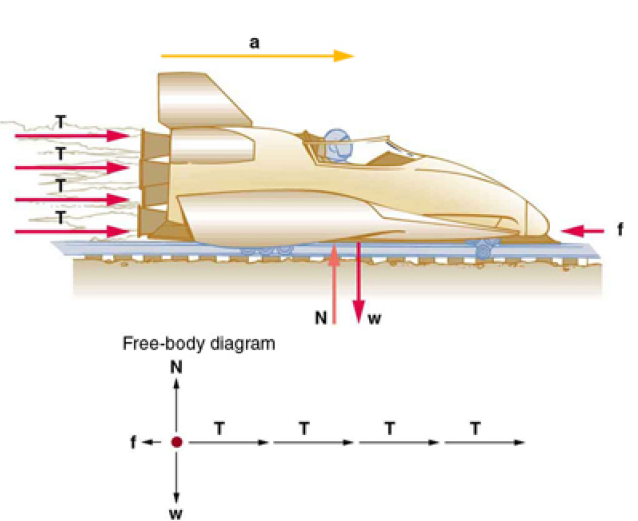
A sled experiences a rocket thrust that accelerates it to the right.Each rocket creates an identical thrust T . As in other situations where there is only horizontal acceleration, the vertical forces cancel. The ground exerts an upward force N on the system that is equal in magnitude and opposite in direction to its weight,w.The system here is the sled, its rockets, and rider, so none of the forces between these objects are considered. The arrow representing friction ( f ) is drawn larger than scale.
Assumptions: The mass of the Sled remains steady throughout the operation

Strategy

Although there are forces acting vertically and horizontally, we assume the vertical forces cancel since there is no vertical acceleration. This leaves us with only horizontal forces and a simpler one-dimensional problem. Directions are indicated with plus or minus signs, with right taken as the positive direction. See the free-body diagram in the figure.

Solution

Since acceleration, mass, and the force of friction are given, we start with Newton’s second law and look for ways to find the thrust of the engines. Since we have defined the direction of the force and acceleration as acting “to the right,” we need to consider only the magnitudes of these quantities in the calculations. Hence we begin with

Fnet is the net force along the horizontal direction, m is the rocket’s mass and a the acceleration.

We can see from the Figure at the top, that the engine thrusts add, while friction opposes the thrust.

Tt is the total thrust from the 4 rockets, Fnet the net force along the horizontal direction and Ff the force of friction.

Finally, since there are 4 rockets, we calculate the thrust that each one provides:

T is the individual Thrust of each engine, b is the number of rocket engines

Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/

In the wheelbarrow of the following figure the load has a perpendicular lever arm of 7.50 cm, while the hands have a perpendicular lever arm of 1.02 m.(a) What upward force must you exert to support the wheelbarrow and its load if their combined mass is 45.0 kg? (b) What force does the wheelbarrow exert on the ground?

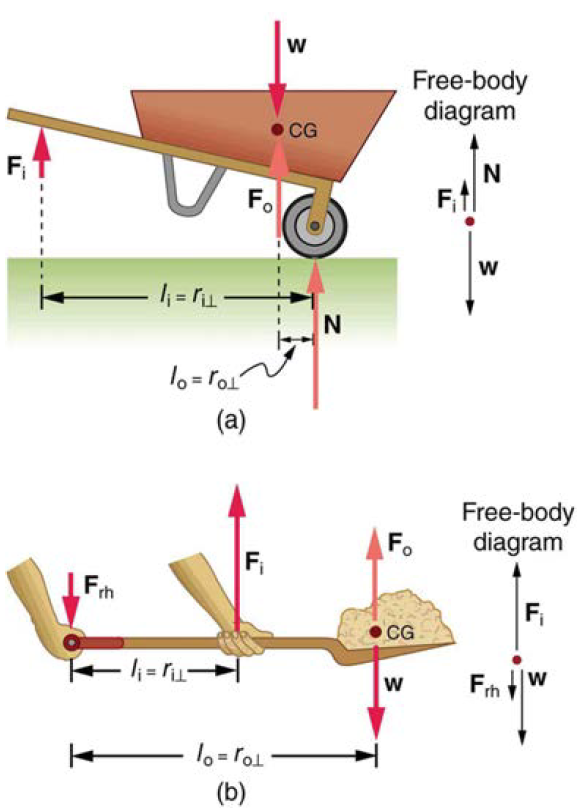
(a) In the case of the wheelbarrow, the output force or load is between the pivot and the input force. The pivot is the wheel’s axle. Here, the output force is greater than the input force. Thus, a wheelbarrow enables you to lift much heavier loads than you could with your body alone. (b) In the case of the shovel, the input force is between the pivot and the load, but the input lever arm is shorter than the output lever arm. The pivot is at the handle held by the right hand. Here, the output force (supporting the shovel’s load) is less than the input force (from the hand nearest the load), because the input is exerted closer to the pivot than is the output.

Strategy

Here, we use the concept of mechanical advantage.

Discussion
An even longer handle would reduce the force needed to lift the load. The MA here is:

Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/

Calculate the change in length of the upper leg bone (the femur) when a 70.0 kg man supports 62.0 kg of his mass on it, assuming the bone to be equivalent to a uniform rod that is 45.0 cm long and 2.00 cm in radius.

Strategy

The force is equal to the weight supported:

and the cross-sectional area of the upper leg bone(femur) is:

To find the change in length we use the Young’s modulus formula. The Young’s modulus reference value for a bone under compression is known to be 9×10⁹ N/m². Now,all quantities except ΔL are known. Thus:

Discussion

This small change in length seems reasonable, consistent with our experience that bones are rigid. In fact, even the rather large forces encountered during strenuous physical activity do not compress or bend bones by large amounts. Although bone is rigid compared with fat or muscle, several of the substances listed in Table 5.3(see reference below) have larger values of Young’s modulus Y . In other words, they are more rigid.

Reference:
This worksheet is a modified version of Example 5.4 page 188 found in :
OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/