Triclinic crystal system (Unit cell's volume)
Description
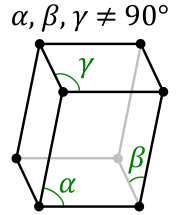
In crystallography, the triclinic crystal system is one of the 7 crystal systems. A crystal system is described by three basis vectors. In the triclinic system, the crystal is described by vectors of unequal length, as in the orthorhombic system. In addition, none of the three vectors are orthogonal to another. The triclinic lattice is the least symmetric of the 14 three-dimensional Bravais lattices. It has (itself) the minimum symmetry all lattices have: points of inversion at each lattice point and at 7 more points for each lattice point: at the midpoints of the edges and the faces, and at the center points. It is the only lattice type that itself has no mirror planes. A crystal is made up of a periodic arrangement of one or more atoms (the basis) repeated at each lattice point. Consequently, the crystal looks the same when viewed from any equivalent lattice point, namely those separated by the translation of one unit cell (the motive). The volume of the unit cell can be calculated by the lattice vectors and the angles between the vectors.
Variables
| Vtr | The volume of the unit cell in triclinic system (Å3) |
| a | Vector (one of the sides of the parallelogram base) (Å) |
| b | Vector (the other side of the parallelogram base) (Å) |
| c | Vector (one of the edges of the side parallelogram plane) (Å) |
| α | Angle between b and c vectors (degree) |
| β | Angle between a and c vectors (degree) |
| γ | Angle between b and a vectors (degree) |