Sum of the ratios on the three altitudes of the distance of the orthocenter from the vertex to the length of the altitude
Description
Altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base (the opposite side of the triangle). This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called the altitude, is the distance between the extended base and the vertex. The three altitudes intersect in a single point, called the orthocenter of the triangle. Denote the vertices of a triangle as A, B, and C and the orthocenter as H, and let D, E, and F denote the feet of the altitudes from A, B, and C respectively. The sum of the ratios on the three altitudes of the distance of the orthocenter from the vertex to the length of the altitude is 2. 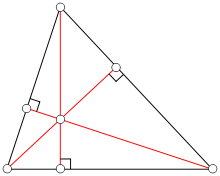
Variables
| AH | Distance of the orthocenter from the vertex A (m) |
| AD | The altitude to the side BC (m) |
| BH | Distance of the orthocenter from the vertex B (m) |
| BE | The altitude to the side AC (m) |
| CH | Distance of the orthocenter from the vertex C (m) |
| CF | The altitude to the side AB (m) |