Relation between the inradius and exradii of a right triangle
Description
Right triangle or right-angled triangle is a triangle in which one angle is a right angle (that is, a 90-degree angle). The incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is called the triangle’s incenter and can be found as the intersection of the three internal angle bisectors. Excircle or exscribed circle of a triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle’s sides. For a right triangle there is a relation between the inradius and exradii of the triangle.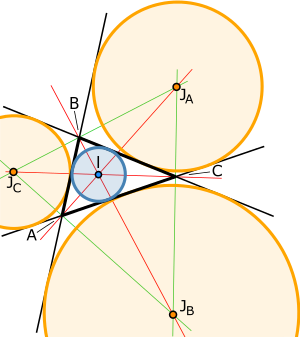
Variables
| r | The inradius of the right triangle (m) |
| ra | The exradius of the excircle tangent to the side a (m) |
| rb | The exradius of the excircle tangent to the side b (m) |
| rc | The exradius of the excircle tangent to the side c (m) |