Pick's theorem
Description
Given a simple polygon constructed on a grid of equal-distanced points (i.e., points with integer coordinates) such that all the polygon’s vertices are grid points, Pick’s theorem provides a simple formula for calculating the area A of this polygon in terms of the number i of lattice points in the interior located in the polygon and the number b of lattice points on the boundary placed on the polygon’s perimeter. ( The theorem is only valid for simple polygons, i.e., ones that consist of a single piece and do not contain “holes”) 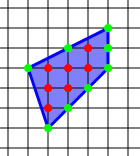
Variables
| A | Area of the polygon (dimensionless) |
| I | The number of lattice points in the interior located in the polygon (dimensionless) |
| B | The number of lattice points on the boundary placed on the polygon's perimeter (dimensionless) |