Pell's equation
Description
Pell’s equation is a Diophantine equation (a polynomial equation in two or more unknowns ).
In Cartesian coordinates, the equation has the form of a hyperbola; solutions occur wherever the curve passes through a point whose x and y coordinates are both integers, such as the trivial solution with x = 1 and y = 0. As long as n is not a perfect square, Pell’s equation has infinitely many distinct integer solutions. These solutions may be used to accurately approximate the square root of n by rational numbers of the form x/y. 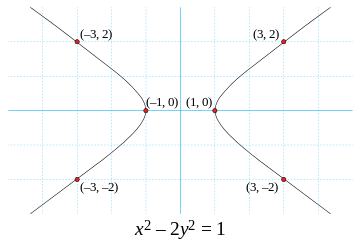
Variables
| x | X- coordinate (dimensionless) |
| n | A nonsquare integer (dimensionless) |
| y | Y- coordinate (dimensionless) |