Paper folding theorem (required strip length for single-direction folding)
Description
Britney Crystal Gallivan (born 1985) of Pomona, California, is best known for determining the maximum number of times that paper or other materials can be folded in half.
Biography
In January 2002, while a junior in high school, Gallivan demonstrated that a single piece of toilet paper 4000 ft (1200 m) in length can be folded in half twelve times. This was contrary to the popular conception that the maximum number of times any piece of paper could be folded in half was seven. She calculated that, instead of folding in half every other direction, the least volume of paper to get 12 folds would be to fold in the same direction, using a very long sheet of paper. A special kind of $85-per-roll toilet paper in a set of six met her length requirement. Not only did she provide the empirical proof, but she also derived an equation that yielded the width of paper or length of paper necessary to fold a piece of paper of thickness t any n number of times.
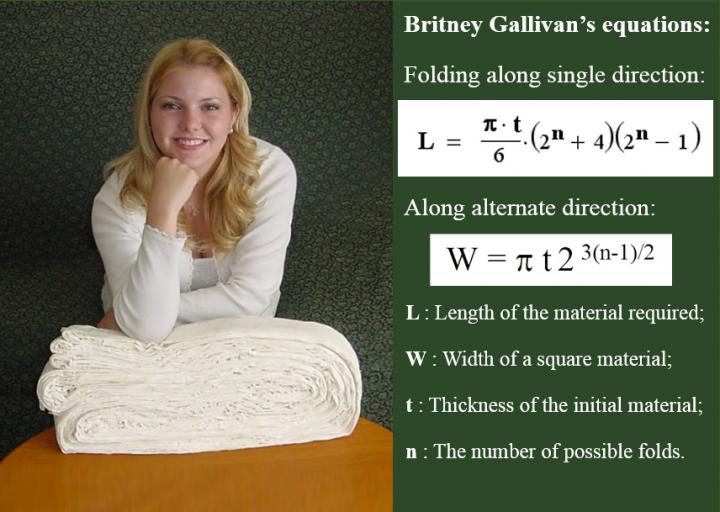
She was a keynote speaker at the September 22, 2006, National Council of Teachers of Mathematics convention.
In 2007, Gallivan graduated from University of California, Berkeley with a degree in Environmental Science from the College of Natural Resources.
Paper folding theorem
For single-direction folding (using a long strip of paper), the exact required strip length L is shown here.
An upper bound and a close approximation of the actual paper width needed for alternate-direction folding can be found here:
Paper folding theorem – required width for alternate-direction folding
In popular culture
Gallivan’s story was mentioned in the episode “Identity Crisis” of Numb3rs, she served as a consultant and was mentioned in an episode of MythBusters3 on the Discovery Channel in 2007, and in episode 3 of QI’s F series.
Variables
| L | length of a paper piece to be folded in only one direction (mm) |
| π | pi |
| t | thickness of the material to be folded (mm) |
| n | number of folds desired (dimensionless) |