Near branch of a hyperbola in polar coordinates with respect to a focal point
Description
In mathematics, a hyperbola is a type of smooth curve, lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. Hyperbola is a conic section, formed by the intersection of a plane and a double cone and the plane intersects both halves of the double cone but does not pass through the apex of the cones. A hyperbola consists of two disconnected curves called its arms or branches. The distance from a point on the left branch of the hyperbola (in canonical form) to the left focal point has polar coordinates depending on the eccentricity of the hyperbola, the semi-major axis and the true anomaly of the point.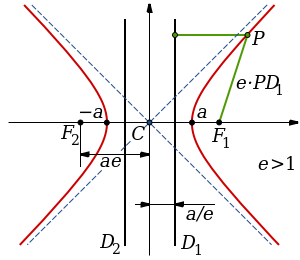
Variables
| r | The distance from the point on the left branch of the hyperbola to the left focal point (m) |
| a | Semi-major axis (m) |
| ϵ | The eccentricity of the hyperbola (dimensionless) |
| θ | The polar angle of the point on the hyperbola relative the near focal point ( true anomaly of the point) (radians) |