Monoclinic crystal system (Unit cell's volume)
Description
In crystallography, the monoclinic crystal system is one of the seven lattice point groups. A crystal system is described by three vectors. In the monoclinic system, the crystal is described by vectors of unequal lengths, as in the orthorhombic system. They form a rectangular prism with a parallelogram as its base. Hence two pairs of vectors are perpendicular, while the third pair makes an angle other than 90°. A crystal is made up of a periodic arrangement of one or more atoms (the basis) repeated at each lattice point. Consequently, the crystal looks the same when viewed from any equivalent lattice point, namely those separated by the translation of one unit cell (the motive). The volume of the unit cell can be calculated by the lattice vectors and the angles between the vectors.
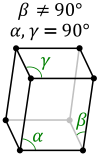
Variables
| Vmon | Unit cell's volume (Å3) |
| a | Vector (one of the sides of the rectangular base) (Å) |
| b | Vector (the other side of the rectangular base) (Å) |
| c | Vector (the edge of the parallelogram side plane) (Å) |
| β | Angle between a and c (degree) |