Linear eccentricity of the hyperbola
Description
Hyperbola is the set of all points in the plane, such that the absolute value of the difference of each of the distances from two fixed points is constant. These fixed points “F1” and “F2” are called “foci”, and on the horizontal hyperbola lie on X-X’ axis. The standard equation of a hyperbola relates (Xv,Yv) vertex coordinates to the coordinates of a point on the hyperbola, the half the distance between the two arms of the hyperbola measured along the major axis and the half distance between the asymptotes along a line tangent to the hyperbola at a vertex. If one calculates the distance from any point on the hyperbola to each focus, the absolute value of the difference of those two distances is always 2a. Eccentricity is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular. Linear eccentricity of hyperbola is the half distance between the foci of the hyperbola and can be calculated by the distance from the center to the vertex (a) and the half distance between the asymptotes (b).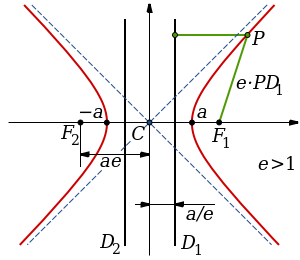
Variables
| c | Linear eccentricity (m) |
| a | Distance from the center to a vertex (m) |
| b | Half the distance between the asymptotes along a line tangent to the hyperbola at a vertex (m) |