Cauchy–Lorentz standar distribution (cumulative distribution function)
Description
In probability and statistics,the Cauchy distribution, is a continuous probability distribution. The simplest Cauchy distribution is called the standard Cauchy distribution. It is the distribution of a random variable that is the ratio of two independent standard normal variables. When U and V are two independent normally distributed random variables with expected value 0 and variance 1, then the ratio U/V has the standard Cauchy distribution.
Its cumulative distribution function F(x; 0,1) has the shape of an arctangent function.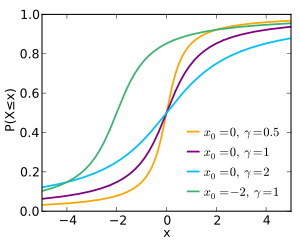
Variables
| F | Cumulative distribution function (dimensionless) |
| π | pi |
| x | Variable (dimensionless) |
| γ | The scale parameter ( γ = 1 ) (dimensionless) |