Cauchy–Lorentz distribution (cumulative distribution function)
Description
In probability and statistics,the Cauchy distribution, is a continuous probability distribution. The Cauchy distribution is often used in statistics as the canonical example of a “pathological” distribution since both its mean and its variance are undefined. The Cauchy distribution does not have finite moments of order greater than or equal to one; only fractional absolute moments exist.The Cauchy distribution has no moment generating function.
Its cumulative distribution function has the shape of an arctangent function( thinking the variables as angles in radians). 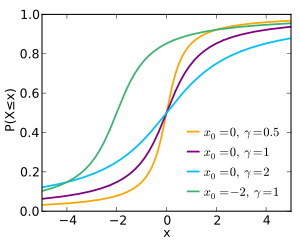
Variables
| Fx | Cumulative distribution function (in a shape of arctanx function) (radians) |
| π | pi |
| x | Variable (radians) |
| x0 | The location parameter, specifying the location of the peak of the distribution (radians) |
| γ | The scale parameter (equal to half the interquartile range) (dimensionless) |