Arbitrary-amplitude period of pendulum
Description
A pendulum is a body suspended from a fixed support so that it swings freely back and forth under the influence of gravity. A so-called “simple pendulum” is an idealization of a “real pendulum” but in an isolated system. The period of a simple harmonic motion depends on the semi-amplitude of the oscillation (that is, the maximum angle between the rod of the pendulum and the vertical) and the length of the pendulum. Under the small-angle approximation, the period is independent of the amplitude θo.
For amplitudes beyond the small angle approximation, one can compute the exact period by first inverting the equation for the angular velocity obtained from the energy method
(The integral diverges as θo approaches the vertical)
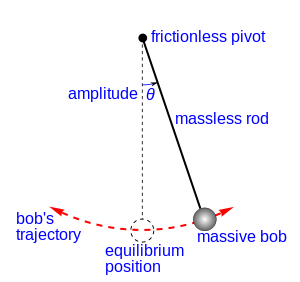
Variables
| T | Period (sec) |
| l | Length (m) |
| g | Standard gravity |
| θ0 | Angle-semi-amplitude of the oscillation (radians) |
| θ | Arbitary angle (radians) |