Search results
In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between ... more
Crest vertical curves are curves which, when viewed from the side, are convex upwards. This includes vertical curves at hill crests, but it also includes ... more
Crest vertical curves are curves which, when viewed from the side, are convex upwards. This includes vertical curves at hill crests, but it also includes ... more
Wafer bonds are commonly characterized by three important encapsulation parameters: bond strength, hermeticity of encapsulation and bonding induced stress. ... more
In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between ... more
Rayleigh scattering (pronounced /ˈreɪli/ RAY-lee), named after the British physicist Lord Rayleigh (John William Strutt), is the (dominantly) elastic ... more
In celestial mechanics, the Lagrangian points (also Lagrange points, L-points, or libration points) are positions in an orbital configuration of two large ... more
Rayleigh scattering (pronounced /ˈreɪli/ RAY-lee), named after the British physicist Lord Rayleigh (John William Strutt), is the (dominantly) elastic ... more
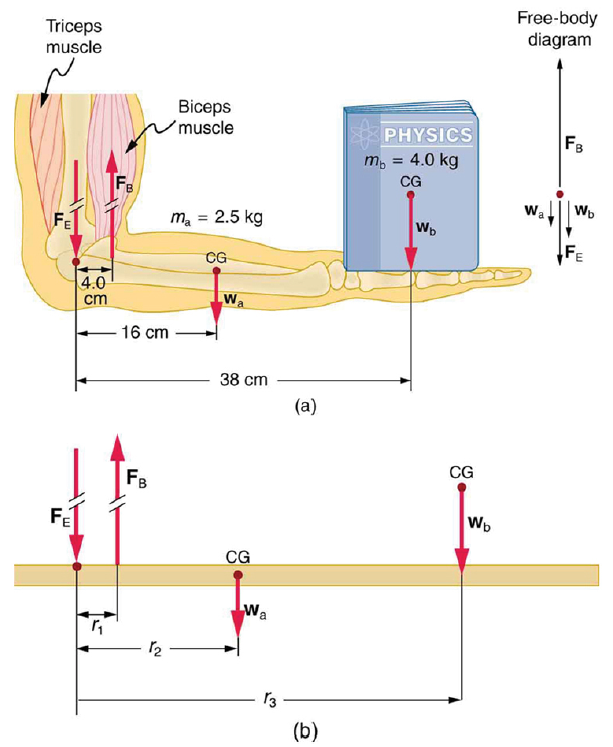
(a) The figure shows the forearm of a person holding a book. The biceps exert a force FB to support the weight of the forearm and the book. The triceps are assumed to be relaxed. (b) Here, you can view an approximately equivalent mechanical system with the pivot at the elbow joint
Strategy
There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is FB, that of the elbow joint is FE, that of the weights of the forearm is wa , and its load is wb. Two of these are unknown FB, so that the first condition for equilibrium cannot by itself yield FB . But if we use the second condition and choose the pivot to be at the elbow, then the torque due to FE is zero, and the only unknown becomes FB .
Solution
The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium (net τ = 0) becomes
Note that sin θ = 1 for all forces, since θ = 90º for all forces. This equation can easily be solved for FB in terms of known quantities,yielding. Entering the known values gives
which yields
Now, the combined weight of the arm and its load is known, so that the ratio of the force exerted by the biceps to the total weight is
Discussion
This means that the biceps muscle is exerting a force 7.38 times the weight supported.
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
In fluid mechanics, the Rayleigh number (Ra) for a fluid is a dimensionless number associated with buoyancy driven flow (also known as free convection or ... more
...can't find what you're looking for?
Create a new formula
Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in the figure below, and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.