Search results
Right triangle or right-angled triangle is a triangle in which one angle is a right angle (that is, a 90-degree angle). The incircle or inscribed circle of ... more
Right triangle or right-angled triangle is a triangle in which one angle is a right angle (that is, a 90-degree angle). The incircle or inscribed circle of ... more
In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is ... more
The law of sines, sine law, sine formula, or sine rule relates the sine of an angle to the opposite side of an arbitrary triangle and the diameter of the ... more
In trigonometry, the law of cotangents is a relationship among the lengths of the sides of a triangle and the cotangents of the halves of the three angles. ... more
The trigonometric functions (also called the circular functions) are functions of an angle. They relate the angles of a triangle to the lengths of its ... more
To rotate the position of the character, we can imagine it as a point on a circle, and we will change the angle of the point by 20 degrees. To do so, we first need to find the radius of this circle and the original angle.
Drawing a right triangle inside the circle, we can find the radius using the Pythagorean Theorem:
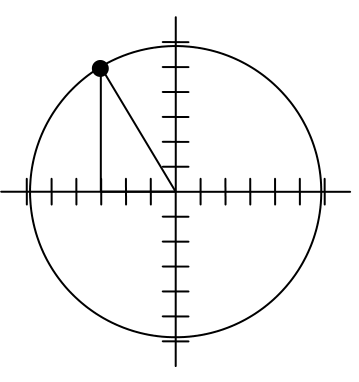
To find the angle, we need to decide first if we are going to find the acute angle of the triangle, the reference angle, or if we are going to find the angle measured in standard position. While either approach will work, in this case we will do the latter. By applying the cosine function and using our given information we get
While there are two angles that have this cosine value, the angle of 120.964 degrees is in the second quadrant as desired, so it is the angle we were looking for.
Rotating the point clockwise by 20 degrees, the angle of the point will decrease to 100.964 degrees. We can then evaluate the coordinates of the rotated point
For x axis:
For y axis:
The coordinates of the character on the rotated map will be (-1.109, 5.725)
Reference : PreCalculus: An Investigation of Functions,Edition 1.4 © 2014 David Lippman and Melonie Rasmussen
http://www.opentextbookstore.com/precalc/
Creative Commons License : http://creativecommons.org/licenses/by-sa/3.0/us/
In surveying, triangulation is the process of determining the location of a point by measuring only angles to it from known points at either end of a fixed ... more
Trapezoid is a convex quadrilateral with only one pair of parallel sides. The parallel sides are called the bases of the trapezoid and the other two sides ... more
In optics, a Gaussian beam is a beam of electromagnetic radiation whose transverse electric field and intensity (irradiance) distributions are well ... more
...can't find what you're looking for?
Create a new formula
In a video game design, a map shows the location of other characters relative to the player, who is situated at the origin, and the direction they are facing. A character currently shows on the map at coordinates (-3, 5). If the player rotates counterclockwise by 20 degrees, then the objects in the map will correspondingly rotate 20 degrees clockwise. Find the new coordinates of the character.