Search results
In mathematics, the Klein bottle is an example of a non-orientable surface, informally, it is a surface (a two-dimensional manifold) in which notions of ... more
The stiffness of a body is a measure of the resistance offered by an elastic body to deformation. A body have a rotational stiffness when it is in a ... more
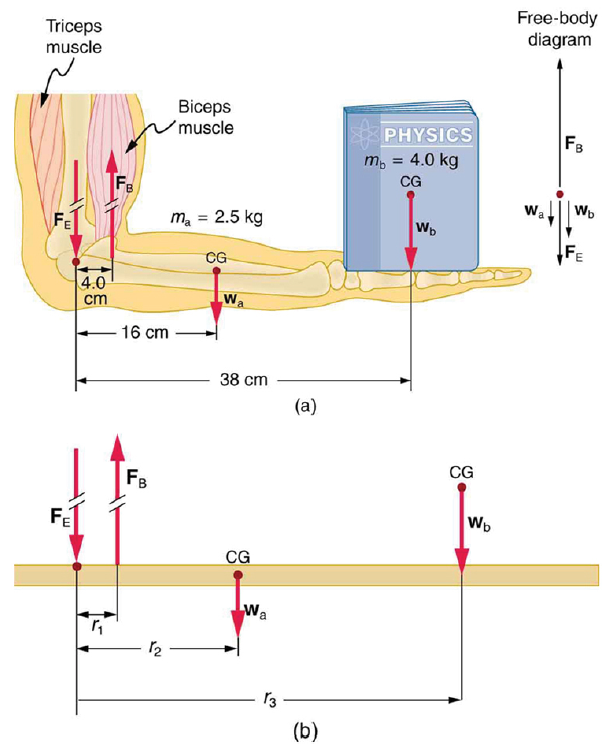
(a) The figure shows the forearm of a person holding a book. The biceps exert a force FB to support the weight of the forearm and the book. The triceps are assumed to be relaxed. (b) Here, you can view an approximately equivalent mechanical system with the pivot at the elbow joint
Strategy
There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is FB, that of the elbow joint is FE, that of the weights of the forearm is wa , and its load is wb. Two of these are unknown FB, so that the first condition for equilibrium cannot by itself yield FB . But if we use the second condition and choose the pivot to be at the elbow, then the torque due to FE is zero, and the only unknown becomes FB .
Solution
The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium (net τ = 0) becomes
Note that sin θ = 1 for all forces, since θ = 90º for all forces. This equation can easily be solved for FB in terms of known quantities,yielding. Entering the known values gives
which yields
Now, the combined weight of the arm and its load is known, so that the ratio of the force exerted by the biceps to the total weight is
Discussion
This means that the biceps muscle is exerting a force 7.38 times the weight supported.
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
The second moment of area, also known as moment of inertia of plane area, area moment of inertia, polar moment of area or second area moment, is a ... more
The second moment of area, also known as moment of inertia of plane area, area moment of inertia, polar moment of area or second area moment, is a ... more
In mathematics, the Klein bottle is an example of a non-orientable surface, informally, it is a surface (a two-dimensional manifold) in which notions of ... more
Harmonic Drive is the brand name of strain wave gear trademarked by the Harmonic Drive company, and invented in 1957 by C.W. Musser.
It is very ... more
The second moment of area, also known as moment of inertia of plane area, area moment of inertia, polar moment of area or second area moment, is a ... more
The second moment of area, also known as moment of inertia of plane area, area moment of inertia, polar moment of area or second area moment, is a ... more
The second moment of area, also known as moment of inertia of plane area, area moment of inertia, polar moment of area or second area moment, is a ... more
...can't find what you're looking for?
Create a new formula
Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in the figure below, and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.