Search results
As used in mechanical engineering, the term tractive force can either refer to the total traction a vehicle exerts on a surface, or the amount of the total ... more
A seiche (/ˈseɪʃ/ SAYSH) is a standing wave in an enclosed or partially enclosed body of water. Seiches and seiche-related ... more
The cross-section of a welded butt joint, with the darkest gray representing the weld or fusion zone, the medium gray the heat affected zone, and the ... more
The R-value is a measure of thermal resistance, or ability of heat to transfer from hot to cold, through materials (such as insulation) and assemblies of ... more
The free-fall time is the characteristic time that would take a body to collapse under its own gravitational attraction, if no other forces existed to ... more
In building and construction,the R-value is a measure of how well an object, per unit of its exposed area, resists conductive flow of heat: the greater the ... more
To rotate the position of the character, we can imagine it as a point on a circle, and we will change the angle of the point by 20 degrees. To do so, we first need to find the radius of this circle and the original angle.
Drawing a right triangle inside the circle, we can find the radius using the Pythagorean Theorem:
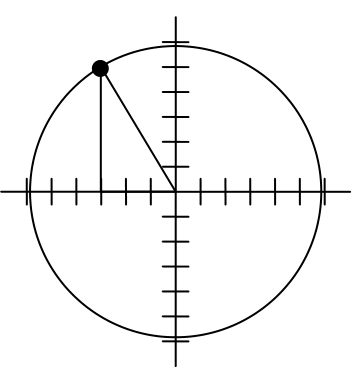
To find the angle, we need to decide first if we are going to find the acute angle of the triangle, the reference angle, or if we are going to find the angle measured in standard position. While either approach will work, in this case we will do the latter. By applying the cosine function and using our given information we get
While there are two angles that have this cosine value, the angle of 120.964 degrees is in the second quadrant as desired, so it is the angle we were looking for.
Rotating the point clockwise by 20 degrees, the angle of the point will decrease to 100.964 degrees. We can then evaluate the coordinates of the rotated point
For x axis:
For y axis:
The coordinates of the character on the rotated map will be (-1.109, 5.725)
Reference : PreCalculus: An Investigation of Functions,Edition 1.4 © 2014 David Lippman and Melonie Rasmussen
http://www.opentextbookstore.com/precalc/
Creative Commons License : http://creativecommons.org/licenses/by-sa/3.0/us/
...can't find what you're looking for?
Create a new formula
In a video game design, a map shows the location of other characters relative to the player, who is situated at the origin, and the direction they are facing. A character currently shows on the map at coordinates (-3, 5). If the player rotates counterclockwise by 20 degrees, then the objects in the map will correspondingly rotate 20 degrees clockwise. Find the new coordinates of the character.