Search results
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
To rotate the position of the character, we can imagine it as a point on a circle, and we will change the angle of the point by 20 degrees. To do so, we first need to find the radius of this circle and the original angle.
Drawing a right triangle inside the circle, we can find the radius using the Pythagorean Theorem:
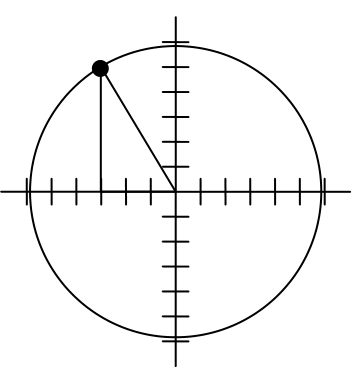
To find the angle, we need to decide first if we are going to find the acute angle of the triangle, the reference angle, or if we are going to find the angle measured in standard position. While either approach will work, in this case we will do the latter. By applying the cosine function and using our given information we get
While there are two angles that have this cosine value, the angle of 120.964 degrees is in the second quadrant as desired, so it is the angle we were looking for.
Rotating the point clockwise by 20 degrees, the angle of the point will decrease to 100.964 degrees. We can then evaluate the coordinates of the rotated point
For x axis:
For y axis:
The coordinates of the character on the rotated map will be (-1.109, 5.725)
Reference : PreCalculus: An Investigation of Functions,Edition 1.4 © 2014 David Lippman and Melonie Rasmussen
http://www.opentextbookstore.com/precalc/
Creative Commons License : http://creativecommons.org/licenses/by-sa/3.0/us/
A right triangle (American English) or right-angled triangle (British English) is a triangle in which one angle is a right angle (that is, a 90-degree ... more
In spherical trigonometry, the law of cosines (also called the cosine rule for sides) is a theorem relating the sides and angles of spherical triangles, ... more
Right triangle or right-angled triangle is a triangle in which one angle is a right angle (that is, a 90-degree angle). The incircle or inscribed circle of ... more
A triangle is a polygon with three edges and three vertices. In a scalene triangle, all sides are unequal and equivalently all angles are unequal. The area ... more
In mathematics, the Pythagorean theorem, also known as Pythagoras’ theorem, is a fundamental relation in Euclidean geometry among the three sides of ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
The trigonometric functions (also called the circular functions) are functions of an angle. They relate the angles of a triangle to the lengths of its ... more
The trigonometric functions (also called the circular functions) are functions of an angle. They relate the angles of a triangle to the lengths of its ... more
The trigonometric functions (also called the circular functions) are functions of an angle. They relate the angles of a triangle to the lengths of its ... more
The trigonometric functions (also called the circular functions) are functions of an angle. They relate the angles of a triangle to the lengths of its ... more
In trigonometry, the law of cotangents is a relationship among the lengths of the sides of a triangle and the cotangents of the halves of the three angles. ... more
A triangle is a polygon with three edges and three vertices. In a scalene triangle, all sides are unequal and equivalently all angles are unequal. When the ... more
The interior perpendicular bisector of a side of a triangle is the segment, falling entirely on and inside the triangle, of the line that perpendicularly ... more
A hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or ... more
Stewart’s theorem yields a relation between the length of the sides of the triangle and the length of a cevian of the triangle. A cevian is any line ... more
In geometry, Napoleon’s theorem states that if equilateral triangles are constructed on the sides of any triangle, either all outward, or all inward, ... more
In spherical trigonometry, the law of cosines (also called the cosine rule for sides) is a theorem relating the sides and angles of spherical triangles, ... more
Morley’s trisector theorem states that in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral ... more
Right triangle or right-angled triangle is a triangle in which one angle is a right angle (that is, a 90-degree angle). The incircle or inscribed circle of ... more
Right triangle or right-angled triangle is a triangle in which one angle is a right angle (that is, a 90-degree angle). The incircle or inscribed circle of ... more
Right triangle or right-angled triangle is a triangle in which one angle is a right angle (that is, a 90-degree angle). The incircle or inscribed circle of ... more
A spherical polygon on the surface of the sphere is defined by a number of great circle arcs which are the intersection of the surface with planes through ... more
Right triangle or right-angled triangle is a triangle in which one angle is a right angle (that is, a 90-degree angle). The incircle or inscribed circle ... more
Morley’s trisector theorem states that in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle, ... more
An angle bisector of a triangle is a straight line through a vertex which cuts the corresponding angle in half. The three angle bisectors intersect in a ... more
...can't find what you're looking for?
Create a new formula
In a video game design, a map shows the location of other characters relative to the player, who is situated at the origin, and the direction they are facing. A character currently shows on the map at coordinates (-3, 5). If the player rotates counterclockwise by 20 degrees, then the objects in the map will correspondingly rotate 20 degrees clockwise. Find the new coordinates of the character.