Search results
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
Snell’s law (also known as the Snell–Descartes law and the law of refraction) is a formula used to describe the relationship between the angles of ... more
Snell’s law (also known as the Snell–Descartes law and the law of refraction) is a formula used to describe the relationship between the angles of ... more
To rotate the position of the character, we can imagine it as a point on a circle, and we will change the angle of the point by 20 degrees. To do so, we first need to find the radius of this circle and the original angle.
Drawing a right triangle inside the circle, we can find the radius using the Pythagorean Theorem:
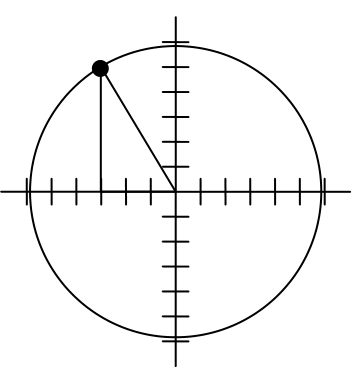
To find the angle, we need to decide first if we are going to find the acute angle of the triangle, the reference angle, or if we are going to find the angle measured in standard position. While either approach will work, in this case we will do the latter. By applying the cosine function and using our given information we get
While there are two angles that have this cosine value, the angle of 120.964 degrees is in the second quadrant as desired, so it is the angle we were looking for.
Rotating the point clockwise by 20 degrees, the angle of the point will decrease to 100.964 degrees. We can then evaluate the coordinates of the rotated point
For x axis:
For y axis:
The coordinates of the character on the rotated map will be (-1.109, 5.725)
Reference : PreCalculus: An Investigation of Functions,Edition 1.4 © 2014 David Lippman and Melonie Rasmussen
http://www.opentextbookstore.com/precalc/
Creative Commons License : http://creativecommons.org/licenses/by-sa/3.0/us/
In a sufficiently narrow tube of circular cross-section of radius “a”, the interface between two fluids forms a meniscus that is a portion of the surface ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
In physics, Bragg’s law, or Wulff–Bragg’s condition, a special case of Laue diffraction, gives the angles for coherent and incoherent ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. If the internal ... more
In Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. It is a four-sided figure in which ... more
In geometry, Napoleon’s theorem states that if equilateral triangles are constructed on the sides of any triangle, either all outward, or all inward, ... more
A quadrilateral is a polygon with four sides (or edges) and four vertices or corners. In any convex quadrilateral ABCD, the ... more
The right triangle altitude theorem or geometric mean theorem is a result in elementary geometry that describes a relation between the altitude on the ... more
The beta angle is a measurement that is used most notably in spaceflight. The beta angle determines the percentage of time an object such as a spacecraft ... more
In Euclidean geometry, a tangential quadrilateral (sometimes just tangent quadrilateral) or circumscribed quadrilateral is a convex quadrilateral whose ... more
In electrical engineering, three-phase electric power systems have at least three conductors carrying alternating current voltages that are offset in time ... more
In mechanical engineering, backlash, sometimes called lash or play, is clearance or lost motion in a mechanism caused by gaps between the parts. It can be ... more
In electrical engineering, three-phase electric power systems have at least three conductors carrying alternating current voltages that are offset in time ... more
In electrical engineering, three-phase electric power systems have at least three conductors carrying alternating current voltages that are offset in time ... more
The alpha helix (α-helix) is a common secondary structure of proteins and is a righthand-coiled or spiral conformation (helix). Residues in α-helices ... more
The capstan equation or belt friction equation, also known as Eytelwein’s formula, relates the hold-force to the load-force if a flexible line is ... more
The minimum railway curve radius, the shortest allowable design radius for railway tracks under a particular set of conditions. It has an important bearing ... more
Precession is a change in the orientation of the rotational axis of a rotating body. In an appropriate reference frame it can be defined as a change in the ... more
calculates the speed of sliding of materials on a gravity conveyer
... more
In electrical engineering, three-phase electric power systems have at least three conductors carrying alternating current voltages that are offset in time ... more
The law of tangents is a statement about the relationship between the tangents of two angles of a triangle and the lengths of the opposing sides.The law of ... more
In crystallography, the monoclinic crystal system is one of the seven lattice point groups. A crystal system is described by three vectors. In the ... more
...can't find what you're looking for?
Create a new formula
In a video game design, a map shows the location of other characters relative to the player, who is situated at the origin, and the direction they are facing. A character currently shows on the map at coordinates (-3, 5). If the player rotates counterclockwise by 20 degrees, then the objects in the map will correspondingly rotate 20 degrees clockwise. Find the new coordinates of the character.