Search results

(a) Calculate the buoyant force on 10,000 metric tons (1.00×10 7 kg) of solid steel completely submerged in water, and compare this with the steel’s weight.

(b) What is the maximum buoyant force that water could exert on this same steel if it were shaped into a boat that could displace 1.00×10 5 m ³ of water?

Strategy for (a)

To find the buoyant force, we must find the weight of water displaced. We can do this by using the densities of water and steel given in Table [insert table #] We note that, since the steel is completely submerged, its volume and the water’s volume are the same. Once we know the volume of water, we can find its mass and weight

First, we use the definition of density to find the steel’s volume, and then we substitute values for mass and density. This gives :

Because the steel is completely submerged, this is also the volume of water displaced, Vw. We can now find the mass of water displaced from the relationship between its volume and density, both of which are known. This gives:

By Archimedes’ principle, the weight of water displaced is m w g , so the buoyant force is:

The steel’s weight is 9.80×10 7 N , which is much greater than the buoyant force, so the steel will remain submerged.

Strategy for (b)

Here we are given the maximum volume of water the steel boat can displace. The buoyant force is the weight of this volume of water.

The mass of water displaced is found from its relationship to density and volume, both of which are known. That is:

The maximum buoyant force is the weight of this much water, or

Discussion

The maximum buoyant force is ten times the weight of the steel, meaning the ship can carry a load nine times its own weight without sinking.

Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/

Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in the figure below, and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.

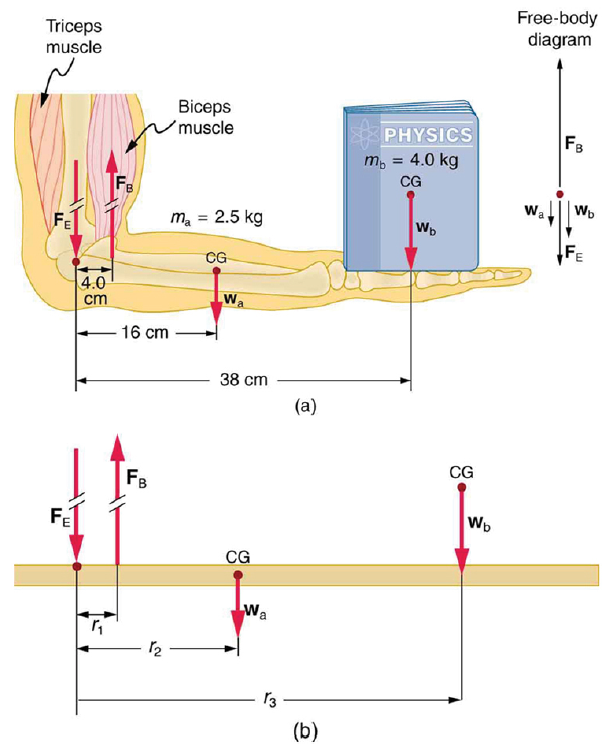
(a) The figure shows the forearm of a person holding a book. The biceps exert a force F_B to support the weight of the forearm and the book. The triceps are assumed to be relaxed. (b) Here, you can view an approximately equivalent mechanical system with the pivot at the elbow joint

Strategy

There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is F_B, that of the elbow joint is F_E, that of the weights of the forearm is w_a , and its load is w_b. Two of these are unknown F_B, so that the first condition for equilibrium cannot by itself yield F_B . But if we use the second condition and choose the pivot to be at the elbow, then the torque due to F_E is zero, and the only unknown becomes F_B .

Solution

The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium (net τ = 0) becomes

Note that sin θ = 1 for all forces, since θ = 90º for all forces. This equation can easily be solved for F_B in terms of known quantities,yielding. Entering the known values gives

which yields

Now, the combined weight of the arm and its load is known, so that the ratio of the force exerted by the biceps to the total weight is

Discussion

This means that the biceps muscle is exerting a force 7.38 times the weight supported.

Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/