Search results
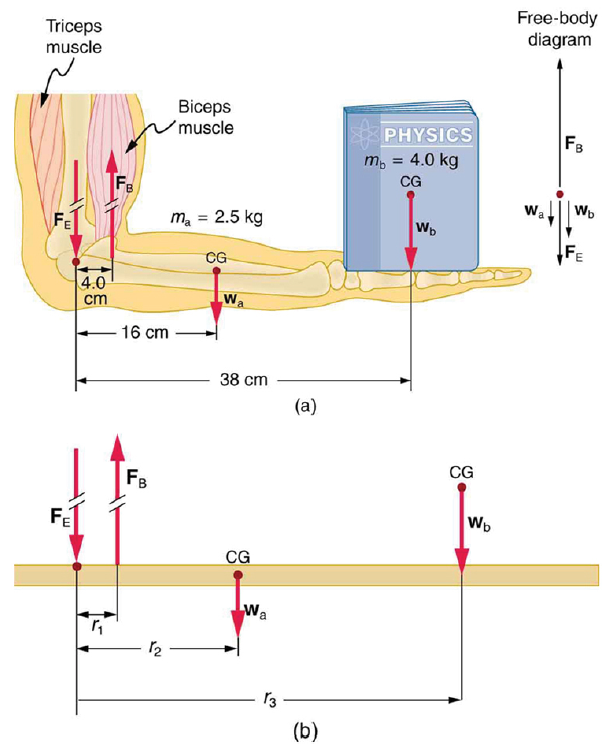
(a) The figure shows the forearm of a person holding a book. The biceps exert a force FB to support the weight of the forearm and the book. The triceps are assumed to be relaxed. (b) Here, you can view an approximately equivalent mechanical system with the pivot at the elbow joint
Strategy
There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is FB, that of the elbow joint is FE, that of the weights of the forearm is wa , and its load is wb. Two of these are unknown FB, so that the first condition for equilibrium cannot by itself yield FB . But if we use the second condition and choose the pivot to be at the elbow, then the torque due to FE is zero, and the only unknown becomes FB .
Solution
The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium (net τ = 0) becomes
Note that sin θ = 1 for all forces, since θ = 90º for all forces. This equation can easily be solved for FB in terms of known quantities,yielding. Entering the known values gives
which yields
Now, the combined weight of the arm and its load is known, so that the ratio of the force exerted by the biceps to the total weight is
Discussion
This means that the biceps muscle is exerting a force 7.38 times the weight supported.
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
In mathematics, a magic cube is the 3-dimensional equivalent of a magic square, that is, a number of integers arranged in a n x n x n pattern such that the ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
Amagat’s law or the Law of Partial Volumes of 1880 describes the behaviour and properties of mixtures of ideal (as well as some cases of non-ideal) ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
The formula is a special case of general Faulhaber’s formula and gives the sum of natural consecutive numbers raised to the fourth power,(starting ... more
he formula is a special case of general Faulhaber’s formula and gives the sum of natural consecutive numbers raised to the fifth power,(starting with 1), ... more
A geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
In mathematics, a magic hypercube is the k-dimensional generalization of magic squares, magic cubes and magic tesseracts; that is, a number of integers ... more
Trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables. Geometrically, ... more
In the gravitational two-body problem, the specific orbital energy (or vis-viva energy) of two orbiting bodies is the constant sum of their mutual ... more
In number theory, the sum of the first n cubes is the square of the nth triangular number. The sequence of squared triangular numbers is
0, 1, 9, ... more
In mathematics, a pyramid number, or square pyramidal number, is a figurate number that represents the number of stacked spheres in a pyramid with a square ... more
In a series configuration, the current through all of the resistors is the same, but the voltage across each resistor will be in proportion to its ... more
In recreational mathematics, a magic square is an arrangement of distinct numbers, usually integers, in a square grid, where the numbers in each row, and ... more
As applied to a rigid body,a standard definition of mechanical equilibrium is:
A rigid body is in mechanical equilibrium when the sum of all forces on
... more
Components of an electrical circuit or electronic circuit can be connected in many different ways. The two simplest of these are called series and parallel ... more
In any convex quadrilateral the sum of the squares of the four sides is equal to the sum of the squares of the two diagonals plus four times the square of ... more
In finance, the net present value or net present worth of a time series of cash flows, both incoming and outgoing, is defined as the sum of the present ... more
Rectangle is any quadrilateral with four right angles. It can also be defined as an equiangular quadrilateral, since equiangular means that all of its ... more
Components of an electrical circuit or electronic circuit can be connected in many different ways. The two simplest of these are called series and parallel ... more
Components of an electrical circuit or electronic circuit can be connected in many different ways. The two simplest of these are called series and parallel ... more
Right triangle or right-angled triangle is a triangle in which one angle is a right angle (that is, a 90-degree angle). The incircle or inscribed circle of ... more
Future value is the value of an asset at a specific date. It measures the nominal future sum of money that a given sum of money is “worth” at a ... more
...can't find what you're looking for?
Create a new formula
Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in the figure below, and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.