Search results
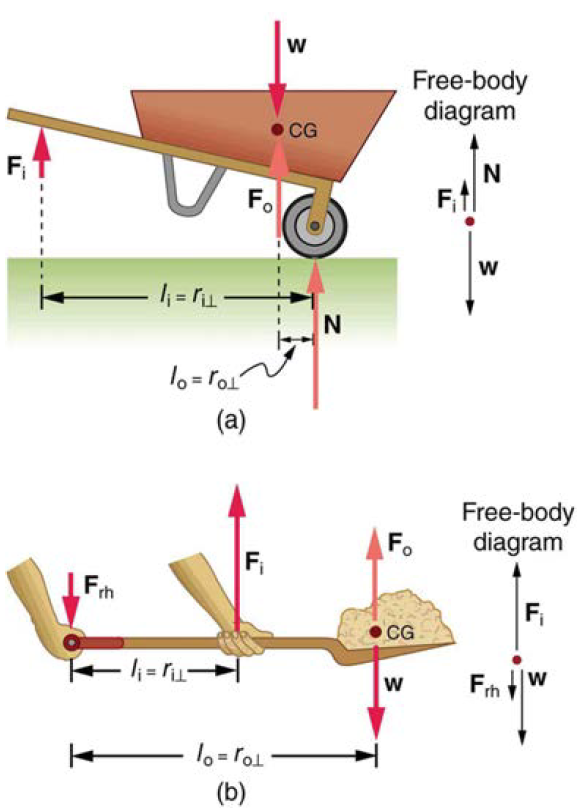
(a) In the case of the wheelbarrow, the output force or load is between the pivot and the input force. The pivot is the wheel’s axle. Here, the output force is greater than the input force. Thus, a wheelbarrow enables you to lift much heavier loads than you could with your body alone. (b) In the case of the shovel, the input force is between the pivot and the load, but the input lever arm is shorter than the output lever arm. The pivot is at the handle held by the right hand. Here, the output force (supporting the shovel’s load) is less than the input force (from the hand nearest the load), because the input is exerted closer to the pivot than is the output.
Strategy
Here, we use the concept of mechanical advantage.
Discussion
An even longer handle would reduce the force needed to lift the load. The MA here is:
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in the figure below, and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.
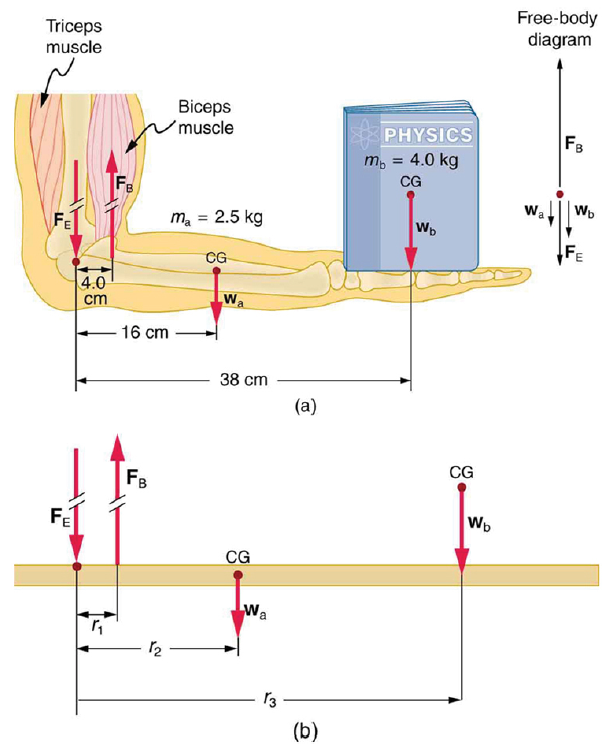
(a) The figure shows the forearm of a person holding a book. The biceps exert a force FB to support the weight of the forearm and the book. The triceps are assumed to be relaxed. (b) Here, you can view an approximately equivalent mechanical system with the pivot at the elbow joint
Strategy
There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is FB, that of the elbow joint is FE, that of the weights of the forearm is wa , and its load is wb. Two of these are unknown FB, so that the first condition for equilibrium cannot by itself yield FB . But if we use the second condition and choose the pivot to be at the elbow, then the torque due to FE is zero, and the only unknown becomes FB .
Solution
The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium (net τ = 0) becomes
Note that sin θ = 1 for all forces, since θ = 90º for all forces. This equation can easily be solved for FB in terms of known quantities,yielding. Entering the known values gives
which yields
Now, the combined weight of the arm and its load is known, so that the ratio of the force exerted by the biceps to the total weight is
Discussion
This means that the biceps muscle is exerting a force 7.38 times the weight supported.
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
Astrology, that unlikely and vague pseudoscience, makes much of the position of the planets at the moment of one’s birth. The only known force a planet exerts on Earth is gravitational.
(a) Calculate the gravitational force exerted on a 4.20 kg baby by a 100 kg father 0.200 m away at birth (he is assisting, so he is close to the child).
(b) Calculate the force on the baby due to Jupiter if it is at its closest distance to Earth, some 6.29e+11 m away. How does the force of Jupiter on the baby compare to the force of the father on the baby?
Father’s gravitational force on the baby is:
Jupiter’s gravitational force on the baby is:
(c) What should be the father’s weight, so that he exerts the same force on the baby as that of Jupiter? **
**this section is not included in the Reference material
Discussion
Other objects in the room and the hospital building also exert similar gravitational forces. (Of course, there could be an unknown force acting, but scientists first need to be convinced that there is even an effect, much less that an unknown force causes it.)Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
Dedicated to little Konstantinos
An example of a function that is solvable for y using standard algebraic techniques, but where approximation methods must be employed to solve for x.
... more
A time value of money calculation is one which solves for one of several variables in a financial problem. In a typical case, the variables might be: a ... more
In mathematics, the gamma function (represented by the capital Greek letter Γ) is an extension of the factorial function, with its argument shifted down by ... more
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers. The ... more
In mathematics, generalised means are a family of functions for aggregating sets of numbers, that include as special cases the arithmetic, geometric, and ... more
The awe‐inspiring Great Pyramid of Cheops was built more than 4500 years ago. Its square base, originally 230 m on a side, covered 13.1 acres, and it was 146 m high (H), with a mass of about 7×10^9 kg. (The pyramid’s dimensions are slightly different today due to quarrying and some sagging). Historians estimate that 20,000 workers spent 20 years to construct it, working 12-hour days, 330 days per year.
a) Calculate the gravitational potential energy stored in the pyramid, given its center of mass is at one-fourth its height.
b) Only a fraction of the workers lifted blocks; most were involved in support services such as building ramps, bringing food and water, and hauling blocks to the site. Calculate the efficiency of the workers who did the lifting, assuming there were 1000 of them and they consumed food energy at the rate of 300 Kcal/hour.
first we calculate the number of hours worked per year.
then we calculate the number of hours worked in the 20 years.
Then we calculate the energy consumed in 20 years knowing the energy consumed per hour and the total hours worked in 20 years.
The efficiency is the resulting potential energy divided by the consumed energy.
...can't find what you're looking for?
Create a new formula
In the wheelbarrow of the following figure the load has a perpendicular lever arm of 7.50 cm, while the hands have a perpendicular lever arm of 1.02 m.(a) What upward force must you exert to support the wheelbarrow and its load if their combined mass is 45.0 kg? (b) What force does the wheelbarrow exert on the ground?