Search results
The arithmetic mean (or simply “mean”) of a sample x1,x2,.x3, ... xn is the sum of the sampled values divided by the number of items in the ... more
conic section (or just conic) is a curve obtained as the intersection of a cone (more precisely, a right circular conical surface) with a plane. A conic ... more
In mathematics, specifically in elementary arithmetic and elementary algebra, given an equation between two fractions or rational expressions, one can ... more
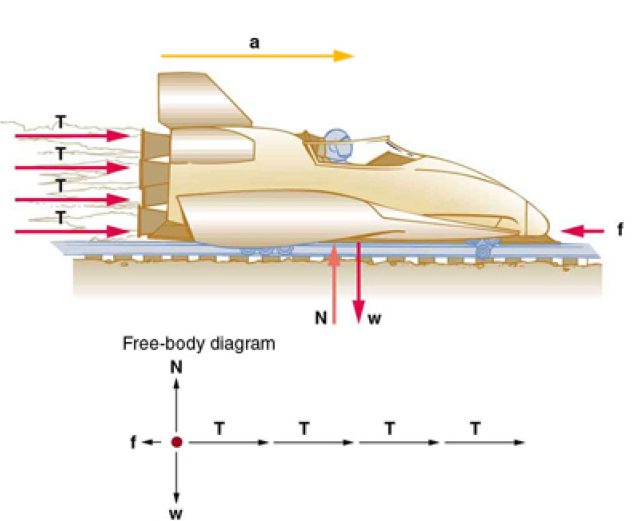
A sled experiences a rocket thrust that accelerates it to the right.Each rocket creates an identical thrust T . As in other situations where there is only horizontal acceleration, the vertical forces cancel. The ground exerts an upward force N on the system that is equal in magnitude and opposite in direction to its weight,w.The system here is the sled, its rockets, and rider, so none of the forces between these objects are considered. The arrow representing friction ( f ) is drawn larger than scale.
Assumptions: The mass of the Sled remains steady throughout the operation
Strategy
Although there are forces acting vertically and horizontally, we assume the vertical forces cancel since there is no vertical acceleration. This leaves us with only horizontal forces and a simpler one-dimensional problem. Directions are indicated with plus or minus signs, with right taken as the positive direction. See the free-body diagram in the figure.
Solution
Since acceleration, mass, and the force of friction are given, we start with Newton’s second law and look for ways to find the thrust of the engines. Since we have defined the direction of the force and acceleration as acting “to the right,” we need to consider only the magnitudes of these quantities in the calculations. Hence we begin with
Fnet is the net force along the horizontal direction, m is the rocket’s mass and a the acceleration.
We can see from the Figure at the top, that the engine thrusts add, while friction opposes the thrust.
Tt is the total thrust from the 4 rockets, Fnet the net force along the horizontal direction and Ff the force of friction.
Finally, since there are 4 rockets, we calculate the thrust that each one provides:
T is the individual Thrust of each engine, b is the number of rocket engines
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
A typical small rescue helicopter, like the one in the Figure below, has four blades, each is 4.00 m long and has a mass of 50.0 kg. The blades can be approximated as thin rods that rotate about one end of an axis perpendicular to their length. The helicopter has a total loaded mass of 1000 kg. (a) Calculate the rotational kinetic energy in the blades when they rotate at 300 rpm. (b) Calculate the translational kinetic energy of the helicopter when it flies at 20.0 m/s, and compare it with the rotational energy in the blades. (c) To what height could the helicopter be raised if all of the rotational kinetic energy could be used to lift it?

The first image shows how helicopters store large amounts of rotational kinetic energy in their blades. This energy must be put into the blades before takeoff and maintained until the end of the flight. The engines do not have enough power to simultaneously provide lift and put significant rotational energy into the blades.
The second image shows a helicopter from the Auckland Westpac Rescue Helicopter Service. Over 50,000 lives have been saved since its operations beginning in 1973. Here, a water rescue operation is shown. (credit: 111 Emergency, Flickr)
Strategy
Rotational and translational kinetic energies can be calculated from their definitions. The last part of the problem relates to the idea that energy can change form, in this case from rotational kinetic energy to gravitational potential energy.
Solution for (a)
We must convert the angular velocity to radians per second and calculate the moment of inertia before we can find Er . The angular velocity ω for 1 r.p.m is
and for 300 r.p.m
The moment of inertia of one blade will be that of a thin rod rotated about its end.
The total I is four times this moment of inertia, because there are four blades. Thus,
and so The rotational kinetic energy is
Solution for (b)
Translational kinetic energy is defined as
To compare kinetic energies, we take the ratio of translational kinetic energy to rotational kinetic energy. This ratio is
Solution for (c)
At the maximum height, all rotational kinetic energy will have been converted to gravitational energy. To find this height, we equate those two energies:
Discussion
The ratio of translational energy to rotational kinetic energy is only 0.380. This ratio tells us that most of the kinetic energy of the helicopter is in its spinning blades—something you probably would not suspect. The 53.7 m height to which the helicopter could be raised with the rotational kinetic energy is also impressive, again emphasizing the amount of rotational kinetic energy in the blades.
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
In a video game design, a map shows the location of other characters relative to the player, who is situated at the origin, and the direction they are facing. A character currently shows on the map at coordinates (-3, 5). If the player rotates counterclockwise by 20 degrees, then the objects in the map will correspondingly rotate 20 degrees clockwise. Find the new coordinates of the character.
To rotate the position of the character, we can imagine it as a point on a circle, and we will change the angle of the point by 20 degrees. To do so, we first need to find the radius of this circle and the original angle.
Drawing a right triangle inside the circle, we can find the radius using the Pythagorean Theorem:
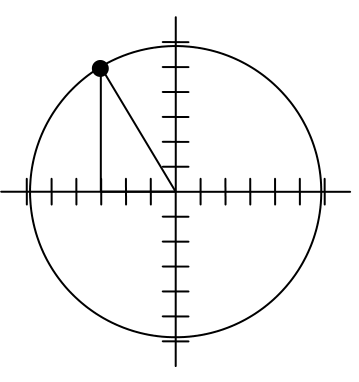
To find the angle, we need to decide first if we are going to find the acute angle of the triangle, the reference angle, or if we are going to find the angle measured in standard position. While either approach will work, in this case we will do the latter. By applying the cosine function and using our given information we get
While there are two angles that have this cosine value, the angle of 120.964 degrees is in the second quadrant as desired, so it is the angle we were looking for.
Rotating the point clockwise by 20 degrees, the angle of the point will decrease to 100.964 degrees. We can then evaluate the coordinates of the rotated point
For x axis:
For y axis:
The coordinates of the character on the rotated map will be (-1.109, 5.725)
Reference : PreCalculus: An Investigation of Functions,Edition 1.4 © 2014 David Lippman and Melonie Rasmussen
http://www.opentextbookstore.com/precalc/
Creative Commons License : http://creativecommons.org/licenses/by-sa/3.0/us/
What is the cost of running a 0.600-kW computer 6.00 h per day for 30.0 d if the cost of electricity is $0.120 per kW ⋅ h ?
where t is the total consumption time, td is the days of consumption and th the hours of consumption per day
where P is Power consumption rate, E is the energy supplied by the electricity company and t is consumption time
keywords:
ballistics
where C is the total cost and CkW is the cost per kilowatt hour
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
In the wheelbarrow of the following figure the load has a perpendicular lever arm of 7.50 cm, while the hands have a perpendicular lever arm of 1.02 m.(a) What upward force must you exert to support the wheelbarrow and its load if their combined mass is 45.0 kg? (b) What force does the wheelbarrow exert on the ground?
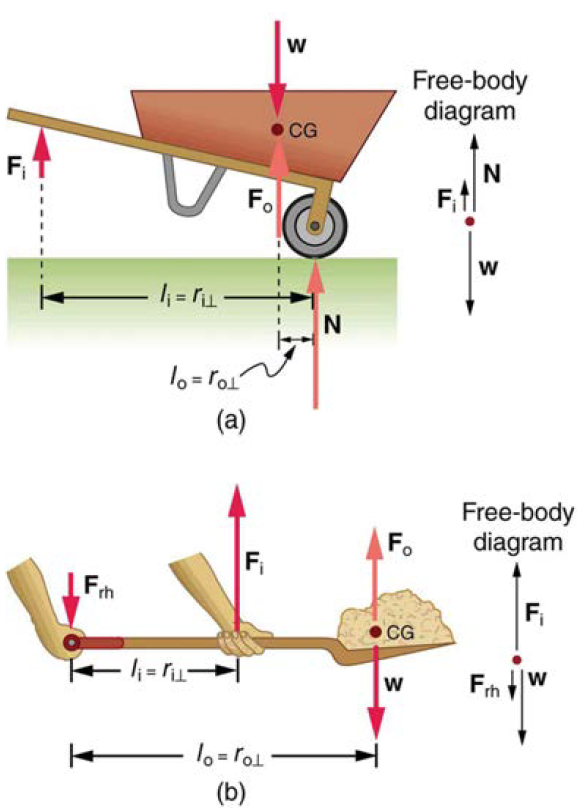
(a) In the case of the wheelbarrow, the output force or load is between the pivot and the input force. The pivot is the wheel’s axle. Here, the output force is greater than the input force. Thus, a wheelbarrow enables you to lift much heavier loads than you could with your body alone. (b) In the case of the shovel, the input force is between the pivot and the load, but the input lever arm is shorter than the output lever arm. The pivot is at the handle held by the right hand. Here, the output force (supporting the shovel’s load) is less than the input force (from the hand nearest the load), because the input is exerted closer to the pivot than is the output.
Strategy
Here, we use the concept of mechanical advantage.
Discussion
An even longer handle would reduce the force needed to lift the load. The MA here is:
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in the figure below, and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.
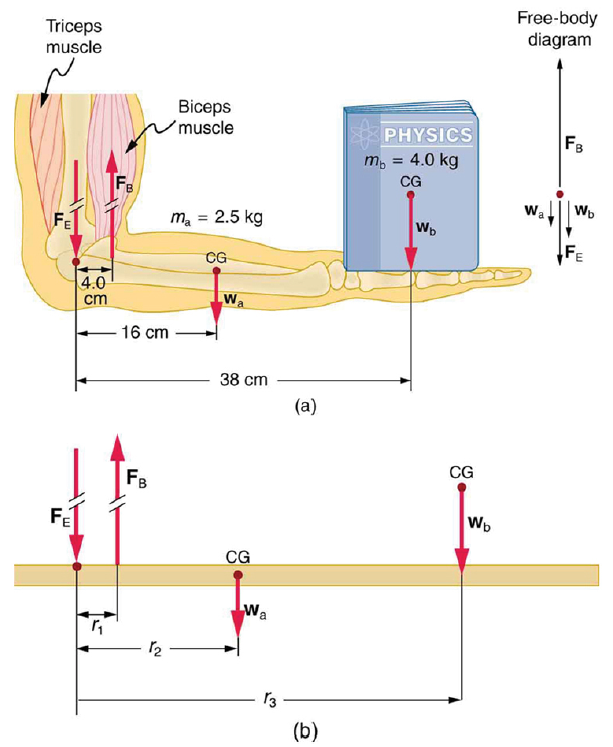
(a) The figure shows the forearm of a person holding a book. The biceps exert a force FB to support the weight of the forearm and the book. The triceps are assumed to be relaxed. (b) Here, you can view an approximately equivalent mechanical system with the pivot at the elbow joint
Strategy
There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is FB, that of the elbow joint is FE, that of the weights of the forearm is wa , and its load is wb. Two of these are unknown FB, so that the first condition for equilibrium cannot by itself yield FB . But if we use the second condition and choose the pivot to be at the elbow, then the torque due to FE is zero, and the only unknown becomes FB .
Solution
The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium (net τ = 0) becomes
Note that sin θ = 1 for all forces, since θ = 90º for all forces. This equation can easily be solved for FB in terms of known quantities,yielding. Entering the known values gives
which yields
Now, the combined weight of the arm and its load is known, so that the ratio of the force exerted by the biceps to the total weight is
Discussion
This means that the biceps muscle is exerting a force 7.38 times the weight supported.
Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
Astrology, that unlikely and vague pseudoscience, makes much of the position of the planets at the moment of one’s birth. The only known force a planet exerts on Earth is gravitational.
(a) Calculate the gravitational force exerted on a 4.20 kg baby by a 100 kg father 0.200 m away at birth (he is assisting, so he is close to the child).
(b) Calculate the force on the baby due to Jupiter if it is at its closest distance to Earth, some 6.29e+11 m away. How does the force of Jupiter on the baby compare to the force of the father on the baby?
Father’s gravitational force on the baby is:
Jupiter’s gravitational force on the baby is:
(c) What should be the father’s weight, so that he exerts the same force on the baby as that of Jupiter? **
**this section is not included in the Reference material
Discussion
Other objects in the room and the hospital building also exert similar gravitational forces. (Of course, there could be an unknown force acting, but scientists first need to be convinced that there is even an effect, much less that an unknown force causes it.)Reference : OpenStax College,College Physics. OpenStax College. 21 June 2012.
http://openstaxcollege.org/textbooks/college-physics
Creative Commons License : http://creativecommons.org/licenses/by/3.0/
Dedicated to little Konstantinos
An example of a function that is solvable for y using standard algebraic techniques, but where approximation methods must be employed to solve for x.
... more
A time value of money calculation is one which solves for one of several variables in a financial problem. In a typical case, the variables might be: a ... more
In mathematics, the gamma function (represented by the capital Greek letter Γ) is an extension of the factorial function, with its argument shifted down by ... more
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers. The ... more
In mathematics, generalised means are a family of functions for aggregating sets of numbers, that include as special cases the arithmetic, geometric, and ... more
The awe‐inspiring Great Pyramid of Cheops was built more than 4500 years ago. Its square base, originally 230 m on a side, covered 13.1 acres, and it was 146 m high (H), with a mass of about 7×10^9 kg. (The pyramid’s dimensions are slightly different today due to quarrying and some sagging). Historians estimate that 20,000 workers spent 20 years to construct it, working 12-hour days, 330 days per year.
a) Calculate the gravitational potential energy stored in the pyramid, given its center of mass is at one-fourth its height.
b) Only a fraction of the workers lifted blocks; most were involved in support services such as building ramps, bringing food and water, and hauling blocks to the site. Calculate the efficiency of the workers who did the lifting, assuming there were 1000 of them and they consumed food energy at the rate of 300 Kcal/hour.
first we calculate the number of hours worked per year.
then we calculate the number of hours worked in the 20 years.
Then we calculate the energy consumed in 20 years knowing the energy consumed per hour and the total hours worked in 20 years.
The efficiency is the resulting potential energy divided by the consumed energy.
In mathematics, the harmonic mean (sometimes called the subcontrary mean) is one of several kinds of average. The harmonic mean is the reciprocal of the ... more
In probability and statistics, mean and expected value are used synonymously to refer to one measure of the central tendency either of a probability ... more
In mathematics, a magic cube is the 3-dimensional equivalent of a magic square, that is, a number of integers arranged in a n x n x n pattern such that the ... more
In mathematics, a magic hypercube is the k-dimensional generalization of magic squares, magic cubes and magic tesseracts; that is, a number of integers ... more
In recreational mathematics, a magic square is an arrangement of distinct numbers, usually integers, in a square grid, where the numbers in each row, and ... more
It is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic (the others being ... more
The normal segment for a given line is defined to be the line segment drawn from the origin perpendicular to the line. This segment joins the origin with ... more
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed ... more
...can't find what you're looking for?
Create a new formula
Prior to manned space flights, rocket sleds were used to test aircraft, missile equipment, and physiological effects on human subjects at high speeds. They consisted of a platform that was mounted on one or two rails and propelled by several rockets. Calculate the magnitude of force exerted by each rocket, called its thrust T , for the four-rocket propulsion system shown in the Figure below. The sled’s initial acceleration is 49 m/s 2, the mass of the system is 2100 kg, and the force of friction opposing the motion is known to be 650 N.