Archimedes of Syracuse was an Ancient Greek mathematician, physicist, engineer, inventor, and astronomer. He is regarded as one of the leading scientists in classical antiquity beside the fact that we know very little about his life.
He is considered one of the greatest mathematicians of all time, and he anticipated modern calculus and analysis by applying concepts of infinitesimals and the method of exhaustion to derive and rigorously prove a range of geometrical theorems, including the area of a circle, the surface area and volume of a sphere, and the trammel of Archimedes.
He has more mathematical achievements under his name, such as deriving an accurate approximation of pi, defining and investigating the spiral bearing his name, and creating a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, founding hydrostatics and statics, including an explanation of the principle of the lever.
The majority of people know him from his famous “Eureka“. The word that he was crying naked in the streets when he invented a method for determining the volume of an object with an irregular shape.
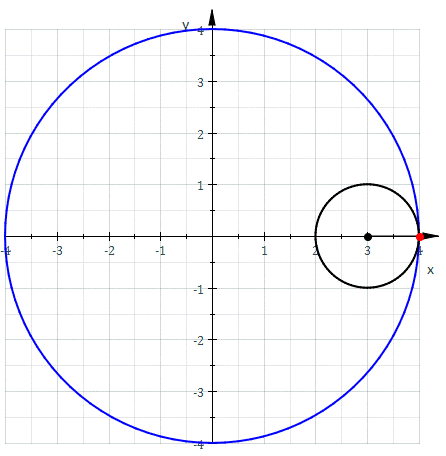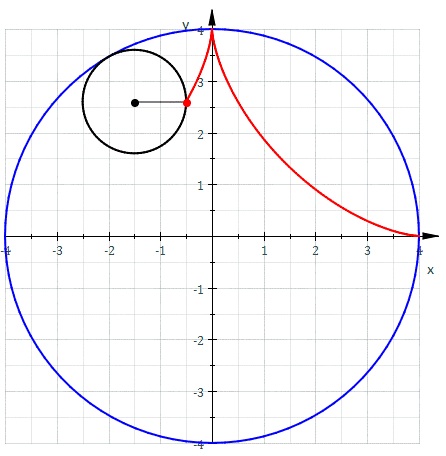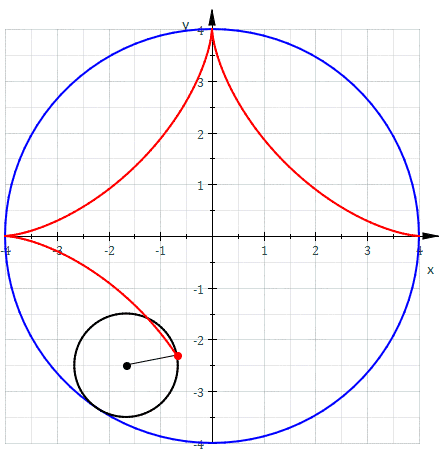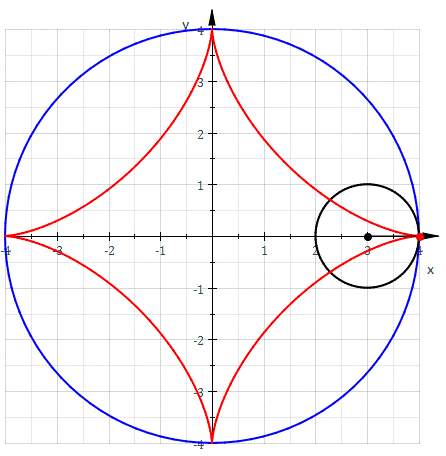
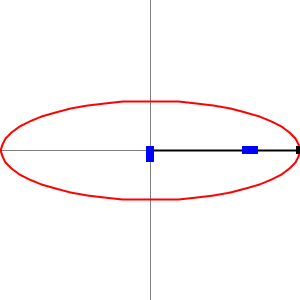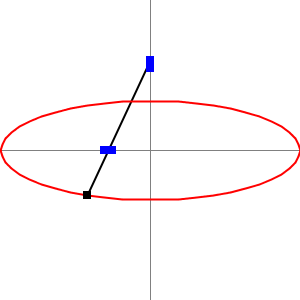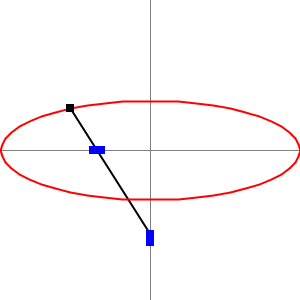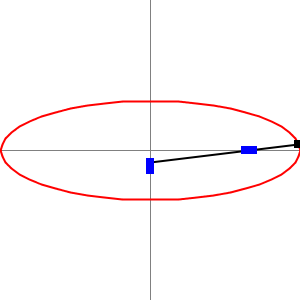
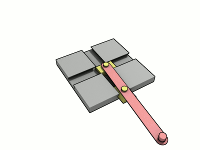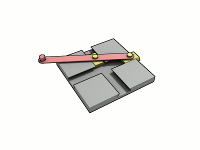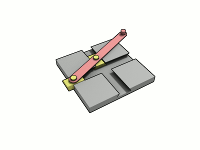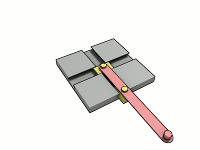
As we mentioned before he invented the “Trammel of his“ (the two .gifs above). It is a mechanism that traces out an ellipse. It consists of two shuttles which are confined (“trammelled”) to perpendicular channels or rails, and a rod which is attached to the shuttles by pivots at fixed positions along the rod. As the shuttles move back and forth, each along its channel, the end of the rod moves in an elliptical path. The semi-axes a and b of the ellipse are the distances between the end of the rod and the two pivots. An ellipsograph is a trammel of Archimedes intended to draw, cut, or machine ellipses, e.g. in wood or other sheet materials. An ellipsograph has the appropriate instrument (pencil, knife, router, etc.) attached to the rod. Usually the distances a and b are adjustable, so that the size and shape of the ellipse can be varied.
The envelope of the moving bar of the Trammel of Archimedes, is the astroid. An astroid is a particular mathematical curve: a hypocycloid with four cusps. The astroid is a real locus of a plane algebraic curve of genus zero. The curve has a variety of names, including tetracuspid, cubocycloid, and paracycle. It is nearly identical in form to the evolute of an ellipse.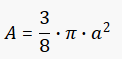
As always, you can try using fxSolver, with the Astroid formula.
Please, remember to follow our social media pages, by hitting the buttons below and watch the fxSolver video as well!